青朱出入图

青朱出入图 《青朱出入图》证明过程是什么？《青朱出入图》证明过程是什么？

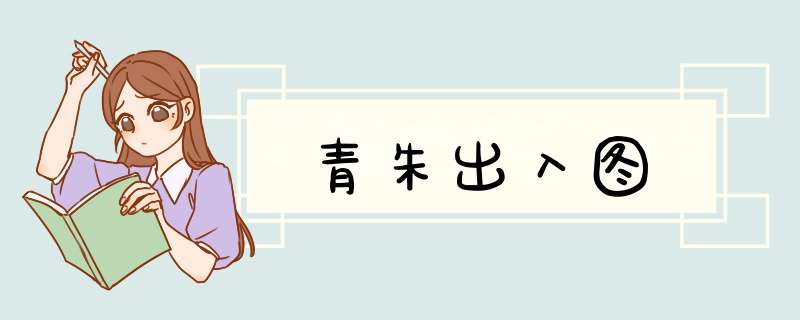
刘徽在证明勾股定理时也是用的以形证数的方法只要把图中朱方（a2）的I移至I′，青方的II移至II′，III移至III′，则刚好拼好一个以弦为边长的正方形（c2 ）．由此便可证得a2+b2=c2这个证明是由三国时代魏国的数学家刘徽所提出的。

在魏景元四年（即公元 263 年），刘徽为古籍《九章算术》作注释。

在注释中，他画了一幅像图五(b)中的图形来证明勾股定理。

只是具体的分合移补略有不同．刘徽的证明原也有一幅图，可惜图已失传，只留下一段文字：“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂．开方除之，即弦也．”后人根据这段文字补了一张图。

大意是：三角形为直角三角形，以勾a为边的正方形为朱方，以股b为边的正方形为青方。

以盈补虚，将朱方、青放并成弦方。

依其面积关系有a^+b^=c^。

由于朱方、青方各有一部分在弦方内，那一部分就不动了。

以勾为边的的正方形为朱方，以股为边的正方形为青方。

以赢补虚，只要把图中朱方（a2）的I移至I′，青方的II移至II′，III移至III′，则刚好拼好一个以弦为边长的正方形（c的平方）．由此便可证得a的平方+b的平方=c的平方。

这个证明是由三国时代魏国的数学家刘徽所提出的。

在魏景元四年（即公元263年），刘徽为古籍《九章算术》作注释。

在注释中，他画了一幅像图五(b)中的图形来证明勾股定理。

由於他在图中以「青出」、「朱出」表示黄、紫、绿三个部分，又以「青入」、「朱入」解释如何将斜边正方形的空白部分填满，所以后世数学家都称这图为「青朱入出图」。

亦有人用「出入相补」这一词来表示这个证明的原理。

青朱出入图的方法