光学光刻和EUV光刻中的掩膜与晶圆形貌效应

　　半导体制造中微型化的进展使得光刻掩膜和晶圆上的几何图形不断增加。准确模拟这些图形产生的衍射要求运用精确的电磁场(EMF)模拟方法。这些方法是在给定的几何形状、材料参数和入射场(照明)条件下，用合适的数值方法解麦克斯韦方程组。

　　时域有限差分法(FDTD)将离散积分格式用于微分形式麦克斯韦方程。此方法非常灵活，易于适应各种不同的几何形状和入射场条件。这一方法的计算结果和精确度主要取决于依据每波长网格点数(GPW) 的空间离散化程度。计算时间和存储要求与模拟体中网格点总数是线性比例关系。很多情况下，为了得到某些现象的直观近场分布图和定性研究，15-25 GPW就足够了。光刻模拟的典型准确度要求多半需要100GPW以上。FDTD已被应用于解决先进光刻中的许多典型问题。

　　像波导法(WGM)和严格耦合波分析(RCWA)一样，模态法也是用切割模拟体、切片内电磁场和光学材料特性的Fourier展开式，以及它们之间Fourier系数的耦合解麦克斯韦方程。散射场是以产生的代数方程式的解获得的。WGM(及类似方法)的计算结果和准确度主要决定于Fourier展开式的阶数(WG阶)和切片数。计算时间和存储要求随WG阶的三次方增加。一般说来，对于求解具有矩形块结构几何形状(如垂直吸收侧壁)的2D问题(线条和隔离)，这些模态法是非常准确而有效的。这些方法缩微化能力差使其难以应用到更大的3D问题(如接触孔的半密矩阵)。已开发了特殊的分解方法解决这一问题。有效执行WGM目前已用于光学和EUV掩膜及晶圆形貌效应的高效模拟。

　　其它EMF模拟方法基于麦克斯韦方程的积分表达式。最近的论文证明，对于模拟形状复杂的掩膜几何图形的光衍射，有限元方法(FEM)和有限积分技术(FIT)具有极高的准确度。这使得这些方法对于标定其它方法和一些特殊场合的模拟非常有用。详细了解和精确模拟从光刻掩膜和晶圆上的(亚)波长尺寸特征图形产生的光衍射，对于开发和优化先进光刻工艺是不可或缺的。

　　掩膜形貌的影响

　　掩膜模型

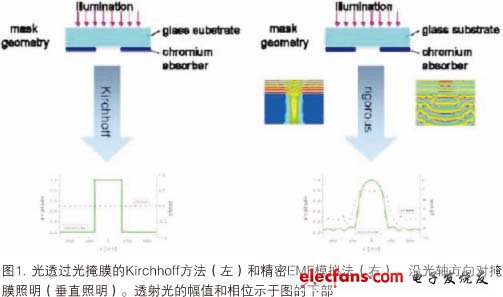
　　图1是光透射通过光掩膜用的二种本质上不同的模拟方法。在Kirchhoff方法中(左图)，透射光的幅值及相位直接由掩膜版图确定。对于所示的二元掩膜，在铬覆盖的区域内，透射光的幅值为0.0，其余地方为1.0。透射光的相位是常数。精密掩膜模型(右图)用麦克斯韦方程的数值解法计算透射光的幅值和相位。通过近场Fourier变换得到掩膜远场内的衍射谱，示于图1的下半部分。光刻成像系统的投影光瞳覆盖一部分衍射谱，并将其转换为晶圆一侧的图形。通常，掩膜是由不同方向照明的。特定照明方向的衍射光可以用二种方法得到：用精密EMF模拟相关的入射光方向;或对于计算前入射光方向的衍射谱进行角度偏移(旋转)(Hopkins法)。对所有相关入射光方向的精密EMF模拟(不用Hopkins法)是最准确而又耗时的。

　　掩膜衍射分析

　　直接分析掩膜衍射谱或掩膜衍射分析可用来识别最重要的掩膜侧散射效应的成像结果，即所谓的掩膜形貌效应。图2显示垂直入射光零级和一级衍射光的模拟衍射效率及这些衍射级间的相位差。

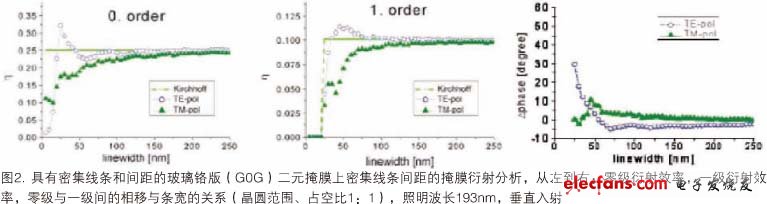
　　对比所谓的薄掩膜或Kirchhoff 法，EMF模拟结果证明掩膜特征尺寸和入射光的极化对衍射光的强度及相位有显著影响。特征尺寸和极化的影响随条宽的减小而增加。对于80nm以下的特征尺寸，可以观察到显著的掩膜引起的相位效应。这些相位效应产生像差一类的结果。