
由CNN驱动的深度学习模型现在无处不在,你会发现它们已散布到全球的各种计算机视觉应用程序中。就像XGBoost和其他流行的机器学习算法一样,卷积神经网络通过黑客马拉松(2012年ImageNet竞赛)进入了公众的意识。
从那时起,这些神经网络就如火一样吸引了灵感,并扩展到各个研究领域。以下是一些使用CNN的流行计算机视觉应用程序:
面部识别系统
通过文档分析和解析
智慧城市(例如交通摄像头)
推荐系统,以及其他用例
但是,为什么卷积神经网络能很好地工作呢?与传统的人工神经网络相比,它的性能如何?为何深度学习专家喜欢它?
要回答这些问题,我们必须了解CNN实际上是如何运作的。在本文中,我们将研究CNN模型背后的数学原理。
神经网络导论
神经网络是所有深度学习算法的核心。但是,在深入研究这些算法之前,对神经网络的概念有一个很好的了解是很重要的。
这些神经网络试图模仿人脑及其学习过程。就像大脑接受输入,对其进行处理并生成一些输出一样,神经网络也是如此。
这三个动作- 接收输入,处理信息,生成输出 -在神经网络中以层的形式表示-输入,隐藏和输出。以下是神经网络的骨架:
这些层中的各个单元称为神经元。神经网络的完整训练过程包括两个步骤。
1.正向传播
图像以数字形式输入到输入层。这些数值表示图像中像素的强度。隐藏层中的神经元对这些值应用了一些数学运算(我们将在本文稍后讨论)。
为了执行这些数学运算,需要随机初始化某些参数值。将这些数学运算发布到隐藏层后,结果将发送到生成最终预测的输出层。
2.向后传播
生成输出后,下一步就是将输出与实际值进行比较。根据最终输出以及该值与实际值(错误)的接近或相距远近,将更新参数的值。使用更新的参数值重复进行前向传播过程,并生成新的输出。
这是任何神经网络算法的基础。在本文中,我们将研究卷积神经网络的向前和向后传播步骤!
卷积神经网络(CNN)架构
考虑一下–您需要在两个给定的图像中识别对象。您将如何去做?通常,您将观察图像,尝试从图像中识别出不同的特征,形状和边缘。根据收集到的信息,您可以说该物体是狗或汽车等。
这正是CNN中的隐藏层所做的–查找图像中的特征。卷积神经网络可以分为两部分:
卷积层:从输入中提取特征
完全连接的(密集)层:使用卷积层中的数据生成输出
正如我们在上一节中讨论的那样,任何神经网络的训练都涉及两个重要过程:
正向传播:接收输入数据,处理信息并生成输出
向后传播:计算误差并更新网络参数
我们将一一介绍这两个方面。让我们从正向传播过程开始。
卷积神经网络(CNN):正向传播
卷积层
您知道我们如何看待图像并识别物体的形状和边缘吗?卷积神经网络通过比较像素值来做到这一点。
下面是数字8的图像以及该图像的像素值。仔细看看图像。您会注意到,数字边缘周围的像素值之间存在显着差异。因此,识别边缘的简单方法是比较相邻像素值。
卷积通常在数学上用星号*表示。如果我们有一个表示为X的输入图像和一个表示为f的滤镜,则表达式为:
Z = X * f
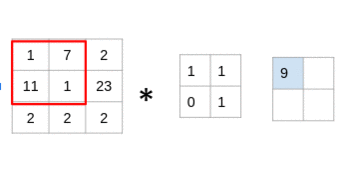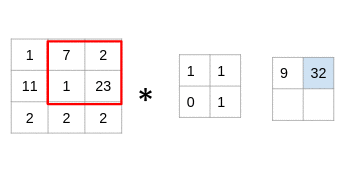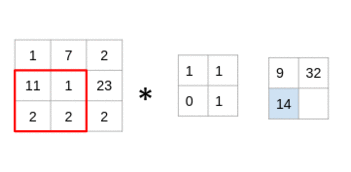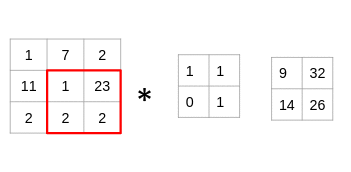
让我们用一个简单的例子来理解卷积的过程。考虑我们有一个尺寸为3 x 3的图像和一个尺寸为2 x 2的滤镜:
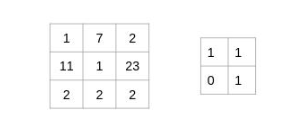
过滤器遍历图像块,执行逐元素乘法,然后将值相加:
(1x1 + 7x1 + 11x0 + 1x1)= 9
(7x1 + 2x1 + 1x0 + 23x1)= 32
(11x1 + 1x1 + 2x0 + 2x1)= 14
(1x1 + 23x1 + 2x0 + 2x1)= 26
仔细看看,您会发现滤镜一次只考虑一小部分图像。我们还可以将其想象成分解为较小补丁的单个图像,每个补丁都与滤镜卷积。

在上面的示例中,我们有一个形状为(3,3)的输入和一个形状为(2,2)的过滤器。由于图像和滤镜的尺寸很小,因此很容易解释输出矩阵的形状为(2,2)。但是,如何为更复杂的输入或过滤器尺寸找到输出的形状?有一个简单的公式可以做到这一点:
图片尺寸=(n,n)
过滤器尺寸=(f,f)
输出的尺寸为((n-f + 1),(n-f + 1))
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)