
简介
现代直接数字频率合成器(DDS)通常利用累加器和数字频率调谐字(FTW)在累加器输出端产生周期性的N位数字斜坡(见图1)。此数字斜坡可依据公式1定义DDS的输出频率(fO),其中fS为DDS采样速率(或系统时钟频率)。
DDS给定时,组成FTW的位数(N)定义了fO的最小可能变化,这发生在FTW值仅更改最低有效位(LSB)时。也就是说,FTW中的1 LSB变化定义了DDS的调谐分辨率。例如,N = 32的DDS的调谐分辨率高于N = 24的DDS。为了证实DDS的极佳调谐能力,以AD9912为例,N = 48产生的调谐分辨率为1/248(即1/281,474,976,710,656)。事实上,fS= 1 GHz时,AD9912产生的频率调谐分辨率约为3.6 µHz(0.0000036 Hz)。
若DDS的FTW为N位,细看图1可知,累加器输出端的位数(N)和角度转幅度模块输入端的位数(P)之间存在明显的差异,即P ≤ N。这种差异会导致DDS输出频谱中出现相位截断杂散。
知道给定DDS的P值对预测相位截断杂散非常重要。本应用笔记介绍了一种用于计算特定相位截断杂散的频率和幅度的方法,尤其适合给定FTW的主相位截断(PPT)。
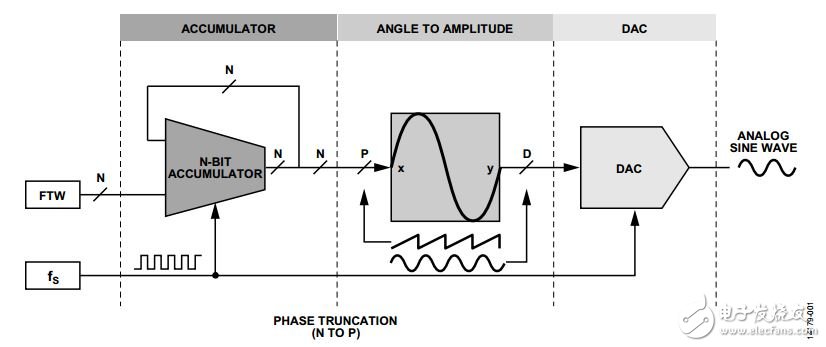
图1. DDS功能框图
相位截断累加器和FTW组成DDS的频率控制元件。但是,除了频率控制元件外,DDS还具有将N位累加器输出从相位值转换为幅度值的角度转幅度模块。角度转幅度模块占据了DDS数字电路的很大一部分。因此,通过增大N来提高DDS的调谐分辨率会大幅增加角度转幅度模块所需的电路数。同样,将所有N位相位信息转换为幅度不太实际。如图1所示,实际DDS使用累加器位的子集进行相位幅度转换,即P最高有效位(MSB)。这种位截断会大幅减少角度转幅度模块所需的电路数。但代价是需要在DDS输出端引入可能的频谱伪像(具体而言就是相位截断杂散)。
相位截断杂散根据定义,按P = N设计的DDS没有相位截断。因此,其输出频谱中没有相位截断杂散。但是在实际DDS中,P < N,这会产生相位截断。
有三类相位截断杂散:一阶、二阶和三阶。这几个分类源于DDS中相位幅度转换器和数模转换器(DAC)的级联组合的频谱特性。图2结合图形说明将傅里叶变换技术应用于角度转幅度模块(带P位相位输入)和呈现谐波失真的非理想DAC所产生的谱线。一般而言,频谱由2P个频率构成,指数范围为0至2P − 1,分类详情如表1。
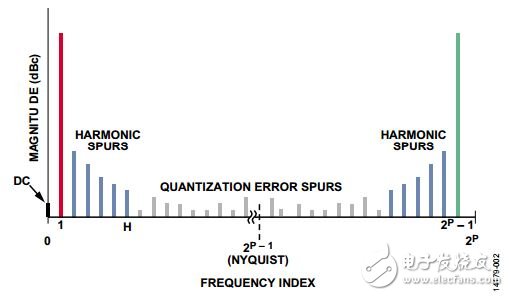
图2. 角度转幅度模块和DAC的频谱特性
主相位截断(PPT)杂散每阶(一阶、二阶和三阶)的许多相位截断杂散可能在DDS的输出频谱中出现,具体取决于FTW的特定值。本应用笔记重点介绍最大的一阶杂散,即PPT杂散。
由于DDS输出是从相位采样生成波形的结果(即累加器输出),因此DDS输出频谱遵循奈奎斯特采样理论的规则。输出频谱显示为两个完全相同的频谱,每个频谱跨越采样频率(fS)一半的频率范围。这两个频谱是彼此的镜像,反映奈奎斯特频率(fS/2)。同样,PPT杂散将其自身表示为两个杂散。一个PPT杂散出现在0 Hz和fS/2之间,另一个作为其镜像出现在fS/2和fS之间。
请注意,尽管两个PPT杂散是最大的一阶相位截断杂散,但整体而言,这些杂散可能不是最大的相位截断杂散。由于相位截断杂散在DDS输出频谱中的分配机制,部分二阶相位截断杂散的幅度可能大于PPT杂散。
我们无法预测二阶或三阶相位截断杂散的幅度。二阶相位截断杂散幅度取决于DAC的谐波失真特性,这些特性因器件而异。三阶相位截断杂散幅度与量化误差相关,而量化误差基本上是随机的。
表1. 图2中显示的频率分类

最右侧的非零位
计算PPT杂散的幅度和频率位置需要知道以下参数:
• DDS采样速率(fS)
• 两个DDS参数:N和P
• FTW的特定值
对于给定应用,N和P固定,fS通常为恒定值。相反,FTW完全可变,控制fO的值(详见公式1)。FTW的值不仅控制DDS输出频谱中fO的位置,而且控制相位截断杂散的位置。事实上,对于DDS输出频谱,给定FTW的最重要特性是以二进制形式表示时的尾随零数量。尾随零数量定义了重要参数L,即FTW最右侧非零位的位置。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)