log 的计算方法

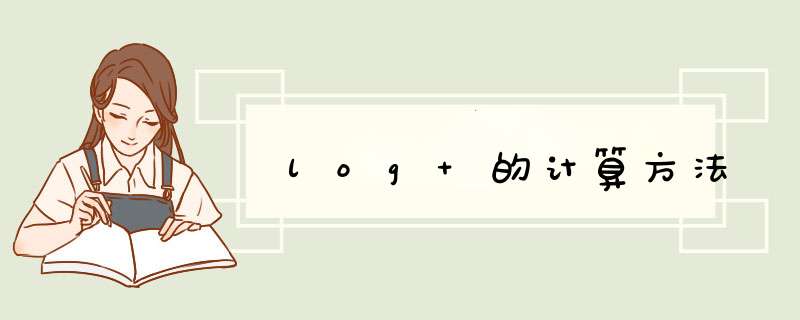
1、a^(log(a)(b))=b

2、log(a)(MN)=log(a)(M)+log(a)(N)

3、log(a)(M÷N)=log(a)(M)-log(a)(N)

4、log(a)(M^n)=nlog(a)(M)

5、lgM=log(10)(M)

扩展资料:

在数学中，对数是对求幂的逆运算，正如除法是乘法的倒数，反之亦然。 这意味着一个数字的对数是必须产生另一个固定数字（基数）的指数。

如果  ，即a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作

 。其中，a叫做对数的底数，N叫做真数，x叫做“以a为底N的对数”。

1、特别地，我们称以10为底的对数叫做常用对数（common logarithm），并记为lg。

2、称以无理数e（e=271828）为底的对数称为自然对数（natural logarithm），并记为ln。

对数函数基本性质

1、过定点  ，即x=1时，y=0。

2、当  时，在  上是减函数；当  时，在  上是增函数。

-对数

对数的加减乘除运算规则：

1、a^(log(a)(b))=b

2、log(a)(a^b)=b

3、log(a)(MN)=log(a)(M)+log(a)(N)；

4、log(a)(M÷N)=log(a)(M)-log(a)(N)；

5、log(a)(M^n)=nlog(a)(M)

6、log(a^n)M=1/nlog(a)(M)

对数在数学内外有许多应用。

这些事件中的一些与尺度不变性的概念有关。例如， *** 的壳的每个室是下一个的大致副本，由常数因子缩放。这引起了对数螺旋。Benford关于领先数字分配的定律也可以通过尺度不变性来解释。对数也与自相似性相关。

例如，对数算法出现在算法分析中，通过将算法分解为两个类似的较小问题并修补其解决方案来解决问题。自相似几何形状的尺寸，即其部分类似于整体图像的形状也基于对数。

对数刻度对于量化与其绝对差异相反的值的相对变化是有用的。此外，由于对数函数log(x)对于大的x而言增长非常缓慢，所以使用对数标度来压缩大规模科学数据。

log 0001=log10^-3=-3

log 0003=log3-3 约为-25（log3大约为05）

log 0115=log115-3 约为-1（log115大约为2）

其实你可以画对数函数图像！当底数大于1的时候，那么在log里面的那个数处于0和1之间，那么就是负的，大于1就是正的！

你好！

掌握好8个公式就行啦，两个特值loga(1)=0,loga(a)=1,对数恒等式a的loga(n)次方=n,三个运算公式loga(MN)=loga(M)+loga(N),loga(M/N)=loga(M)-loga(N),loga(b的n次方）=n(当a=b时,可把任一数化为对数式），

希望对你有所帮助，望采纳。

log函数运算公式是y=logax（a>0 & a≠1）。

对数公式是数学中的一种常见公式，如果a^x=N(a>0，且a≠1)，则x叫作以a为底N的对数，记做x=log(a)(N)，其中a要写于log右下。其中a叫作对数的底，N叫作真数。通常我们将以10为底的对数叫作常用对数，以e为底的对数称为自然对数。

特殊运算

如果a(a大于0,且a不等于1)的b次幂等于N，那么数b叫作以a为底N的对数，记作log aN=b,读作以a为底N的对数，其中a叫作对数的底数，N叫作真数一般地，函数y=log(a)X,(其中a是常数，a>0且a不等于1)叫作对数函数 它实际上就是指数函数的反函数。