函数增长率是2ω2+3ω+1

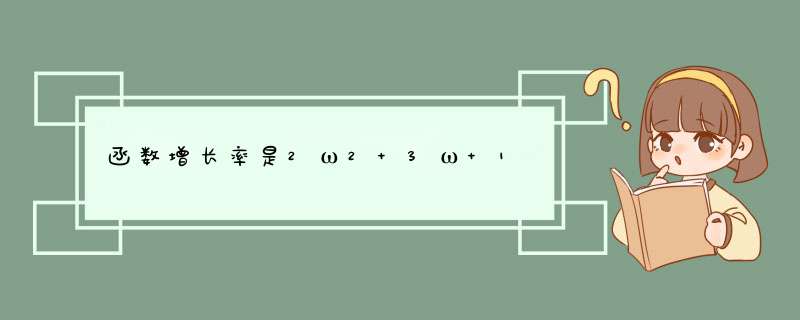
f(x)=2cos^2ωx+2√3sinωx cosωx+3

=cos2ωx+√3sin2ωx +4

=2sin(2ωx+π/6)+4

(1)因为 T=2π/2ω=π 所以 ω=1

(2) f(x)=2sin(2x+π/6)+4

单调增为2kπ-π/2≤2x+π/6≤2kπ+π/2

2kπ-4π/6≤2x≤2kπ+2π/6

kπ-π/3≤x≤kπ+π/6 (k∈Z)

单调减为2kπ+π/2≤2x+π/6≤2kπ+3π/2

2kπ+2π/6≤2x≤2kπ+8π/6

kπ+π/6≤x≤kπ+2π/3 (k∈Z)

故 函数f(x)的单调递增区间：[kπ-π/3,kπ+π/6] (k∈Z)

同理可得：函数f(x)的单调递减区间：[kπ+π/6,kπ+2π/3] (k∈Z)

平均增长率公式a-b/1+b是：求平均数，且是增长率的计算。a是A的增长率；b是B的增长率。

基期平均数：求平均数，问题时间在材料时间之前。A/B×1+b /1+a。a是A的增长率；b是B的增长率。

平均数的增长量：求平均数，且题干出现了两个时间的对比。A/B ×a-b /1+a。a是A的增长率；b是B的增长率。

现期平均数：求平均数，问题时间和材料时间一致。A/B。A代表的是“总数”；B代表的是“份数”。

增长函数算法：混合增长率的公式：r=(1+r1)(1+r2)-1=r1+r2+r1×r2。

两期比重差公式：（A/B)×(a-b)/(1+a)，注意a为分子的增速，b为分母的增速。

相关内容解释：

环比增长率=（本期的某个指标的值-上一期这个指标的值）/上一期这个指标的值100%。比如，2008年5月与2008年4月的环比增长是指总是以上一期为基期求的增长量（或率），一般会列一个表，把若干年的环比增长都列出来，进行分析比较。

定基增长率：如果观察的是若干个时期的数据，每个时期的数据均与同一个基期数据进行对比，则这种比较方法，称为定基比较。例如，将某一时期1970年、1980年、1990年和2000年的GNP数值与1949年进行比较，所获得的4个比例，称为定基增长率。

数学里常说的是平均变化率和函数的平均变化率

如对于f(x)，△x=x2-x1，△y=y2-y1，那么△y/△x就是f（x）在（x1，x2）上的平均变化率

平均增长率和函数的平均变化率，就像映射和函数的关系，都是把大的概念，抽象成数学内容

讲得不太清楚，建议你找一下高中导数第一节的课件学案什么的来看看，应该有更深的理解的，资料可以到百度文库里面找

希望能帮到你！