不同路径I II III js

不同路径I

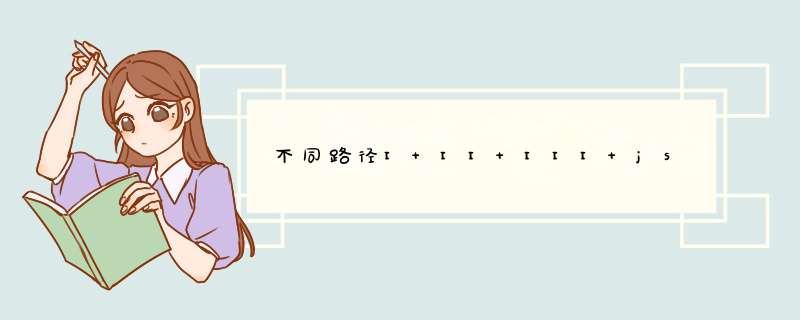
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例1： 

输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

---

解题思路：

机器人只能向下或向右移动，那么说明到达终点位置的路径要么是从左边路径过来，要么是从上边路径过来。我们可以尝试用动态规划来解题。

d数组含义：dp数组表示表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。确定动态规划转移方程：想要求dp[i][j]，只能有两个⽅向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。那么很自然，到达dp[i][j]位置路径就是由二者相加得到。dp数组的初始化：我们观察第一行和第一列，由于机器人不可能往上走，那么机器人肯定只能往右走才能走到第一行的其他位置上，可以得到dp[0][j]为1，因为走到第一行任何一个位置上只能是有从左边走过来这一种情况，因此第一行的路径数都为1。同理：第一列的位置上都只能由上面走来，因此dp[i][0] = 1。确定遍历顺序：这⾥要看⼀下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上⽅和左⽅推导⽽来，那么从左到右⼀层⼀层遍历就可以了。这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]⼀定是有数值的。推导dp数组图表：m=3 , n = 7

1	1	1	1	1	1	1
1	2	3	4	5	6	7
1	3	6	10	15	21	28

这里再次回想下dp数组的含义：dp数组表示表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。那么我们求到终点的路径，就是求dp[m-1][n-1]

 代码：

var uniquePaths = function(m, n) {
    const dp = new Array(m).fill(0).map(()=>new Array(n).fill(0))
    //初始化 *** 作
    for(let i = 0 ; i < m ; i++) dp[i][0] = 1
    for(let j = 0 ; j < n ; j++) dp[0][j] = 1
    for(let i = 1 ; i < m ; i++) {
        for(let j = 1 ; j < n ;j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1]
        }
    }
    return dp[m-1][n-1]
};

 

 不同路径II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2：
输入：obstacleGrid = [[0,1],[0,0]]
输出：1

---

解题思路：

1.本题和上题有区别，在网格中有障碍物，这意味着有障碍物的地方无法行走到，意思就是走到障碍物位置的路径为0。

2.在初始化的时候，我们得考虑到障碍物如果在第一行或者第一列，那么就走不到这个位置了，因此如果第一行或第一列的位置上有障碍物，那么就不能将这个位置的dp初始化为1。

3.如果该位置有障碍物，那么该位置的dp就为0，但初始化时我们将所有位置都填充0了，所以这一步可以省略。

 代码：

var uniquePathsWithObstacles = function(obstacleGrid) {
    let m = obstacleGrid.length , n = obstacleGrid[0].length
    let dp = new Array(m).fill(0).map(()=>new Array(n).fill(0))
    //初始化边界，第一行和第一列分别都只能向右、向下走，前提条件是该位置上没有障碍物，
    //也就是为0。
    for(let i = 0 ; i < m && obstacleGrid[i][0] === 0; i++) 
    {
        dp[i][0] = 1
    }
    for(let j = 0 ; j < n && obstacleGrid[0][j] === 0; j++)
    {
        dp[0][j] = 1
    }
    for(let i = 1 ; i < m ; i++) {
        for(let j = 1 ; j < n ;j++) {
            if(obstacleGrid[i][j] == 0) 
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
            }
            // 这一步可以省略，因为初始化dp数组的时候已经将dp数组的是都填充为0了。
            // else if(obstacleGrid[i][j] == 1)
            // {
            //     dp[i][j] = 0 
            // }
        }
    }
    return dp[m-1][n-1]
};

不同路径III

在二维网格 grid 上，有 4 种类型的方格：

1 表示起始方格。且只有一个起始方格。
2 表示结束方格，且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。
返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2：

输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3：

输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

---

解题思路：

1.题目要求每一个无障碍的方格都要通过，一条完整的路径是除去障碍物剩余的其他方格都走过的。因此需要一个变量count，来记录除去障碍物后需要走的方格数。

2.题目中还说了，一条路径中不能重复通过同一个方格。因此需要在走过这个格子时，将这个格子设置为-1，因为不能走了，因此将走过的格子看作是障碍物。

3.当我们走过的格子数量和出去障碍物剩余的格子数量相等，那么说明我们已经走完了一条路径。找到了一条符合要求的路径，记录下来。

4.grid[row][cor] == 2 && step < count的意思是走到了终点，但是没有走满全部格子。

5.grid[row][cor] == 1 && step != 1意思是并不是起始位置开始走，而是走到了起始位置。

6.因为这个机器人可以上下左右都走，因此递归四个方向。

代码： 

var uniquePathsIII = function(grid) {
    let count = 0 , m = grid.length , n = grid[0].length
    let i0 = -1 , j0 = -1 , res = 0
    //寻找起点并记录障碍物的个数
    for(let i = 0 ; i < m ; i++) {
        for(let j = 0 ; j < n ; j++) {
            if(grid[i][j] == -1) {
                count++
            }else if(grid[i][j] == 1) {
                [i0,j0] = [i,j]
            }
        }
    }
    count = m * n - count
    function backTracking(step,row,cor) {
        if(row<0 || cor<0 ||row>=m || cor>=n || grid[row][cor] == 1 && step != 1 || grid[row]    [cor] == -1 || grid[row][cor] == 2 && step < count) {
            return 
        }else if(count == step) {
            res++
            return
        }
        grid[row][cor] = -1
        backTracking(step+1,row-1,cor)
        backTracking(step+1,row,cor+1)
        backTracking(step+1,row+1,cor)
        backTracking(step+1,row,cor-1)
        grid[row][cor] = 0
    }

    backTracking(1,i0,j0)
    return res
};