排列组合A几几的 C几几的怎么算

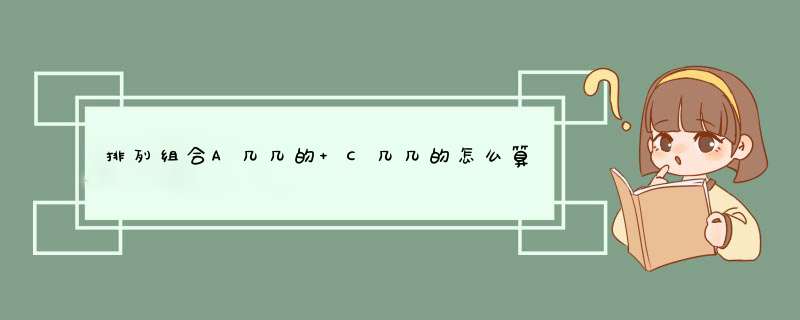
例如  A3 2 (3在下面2在上面）=32=6

C3 2 (3在下面2在上面）=（32）/（21）=3

它的计算公式是这样的：

扩展资料：

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。 排列组合与古典概率论关系密切。

C语言中实现阶乘的计算可以采用递归或者循环，通常循环用的比较多，循环可以采用while循环和for循环等。

下面以for循环为例实现1-10的阶乘的和的计算，代码如下：

int i,sum=1,S=0; 

for(i=1;i<=10;i++)

{

sum=sumi;

S=S+sum;

}

上述的变量S在运行结束后的结果值即为1-10的阶乘的和。

扩展资料：

数学函数

所在函数库为mathh、stdioh、stringh、floath

int abs(int i) 返回整型参数i的绝对值

double atof(char nptr) 将字符串nptr转换成浮点数并返回这个浮点数

double atoi(char nptr) 将字符串nptr转换成整数并返回这个整数

double atol(char nptr) 将字符串nptr转换成长整数并返回这个整数

char ecvt(double value,int ndigit,int decpt,int sign)，将浮点数value转换成字符串并返回该字符串

参考资料来源：百度百科-C语言函数

n的阶乘的通项公式为n！=1×2×3×…×n。

一个正整数的阶乘是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。1808年，基斯顿·卡曼引进这个表示法。

由于正整数的阶乘是一种连乘运算，而0与任何实数相乘的结果都是0。所以用正整数阶乘的定义是无法推广或推导出0！=1的。复数阶乘存在路径问题，路径不同阶乘的结果就不相同，幅角a相等是指按直线从0点附近到z，不等时是按曲线取阶乘。

定义范围

通常我们所说的阶乘是定义在自然数范围里的（大多科学计算器只能计算 0～69 的阶乘），小数科学计算器没有阶乘功能，如 05！，065！，0777！都是错误的，但是，有时候我们会将Gamma 函数定义为非整数的阶乘，因为当 x 是正整数 n 的时候，Gamma 函数的值是 n－1 的阶乘。

1、不是直接输入n！，需要一定的算法才可以实现。具体方法是，首先打开编辑器，准备好空白的C语言文件：

2、在编辑器中输入代码，这里所谓 n 的阶乘，就是从 1 开始乘以比前一个数大 1 的数，一直乘到 n。C语言中可利用循环解决，可以假设循环变量为 i，初值为 1，i 从 1 变化到 n；依次让 i 与 sum 相乘，并将乘积赋给 sum，最后输出sum的值就可以了：

3、在编辑器中运行程序，随意输入一个数，按下回车键，即可打印出阶乘的结果来：

大写字母C,下标n,上标m,表示从n个元素中取出m 个元素的不同的方法数如从5个人中选2人去开会,不同的选法有C(5,2)=10种。

C(n,m)的计算方法是C(n,m)=n!/[m!(n-m)!]=n(n-1)(n-m+1)/[12m]，如C(5,2)=[54]/[12]=10。

扩展资料：

1772年，法国数学家范德蒙德（Vandermonde， A - T）以[n]p表示由n个不同的元素中每次取p个的排列数。

瑞士数学家欧拉（Euler， L）则于1771年以 及于1778年以 表示由n个不同元素中每次取出p个元素的组合数。

1830年，英国数学家皮科克（Peacock， G）引入符号Cr表示n个元素中每次取r个的组合数。

1869年或稍早些，剑桥的古德文以符号nPr 表示由n个元素中每次取r个元素的排列数，这用法亦延用至今。按此法，nPn便相当于n！。

1872年，德国数学家埃汀肖森（Ettingshausen，B A von）引入了符号（np）来表示同样的意义，这组合符号（Signs of Combinations）一直沿用至今。

1880年，鲍茨（Potts ， R）以nCr及nPr分别表示由n个元素取出r个的组合数与排列数。

1886年，惠特渥斯（Whit-worth， A W）用Cnr和Pnr表示同样的意义，他还用Rnr表示可重复的组合数。

1899年，英国数学家、物理学家克里斯托尔（Chrystal，G）以nPr，nCr分别表示由n个不同元素中每次取出r个不重复之元素的排列数与组合数，并以nHr表示相同意义下之可重复的排列数，这三种符号也通用至今。

1904年，德国数学家内托（Netto， E）为一本百科辞典所写的辞条中，以Arn表示上述nPr之意，以Crn表示上述nCr之意，后者亦也用符号（n r）表示。这些符号也一直用到现代。

参考资料来源：百度百科-排列组合

数学组合公式C（n，m）=A（n，m）/m！，组合数公式是指从n个不同元素中，任取m（m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

---