100内的质数是有哪些

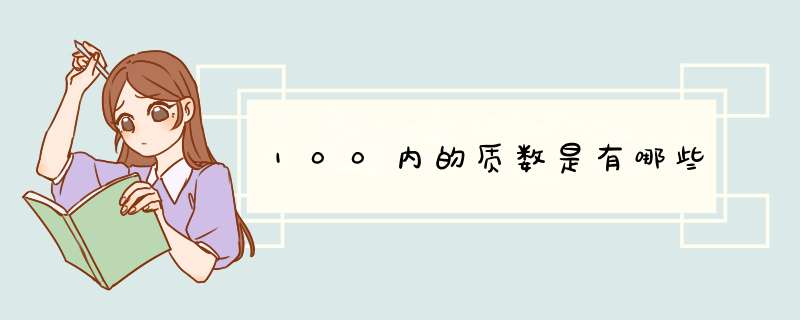
100以内的质数有如下25个数，可以用下面两种方式快速记住或找到：

100以内质数表

① 口诀法：

二三五七和十一，十三后面是十七，还有十九别忘记，二三九，三一七，四一四三四十七，五三九，六一七，七一七三七十九，八三八九九十七。

100以内质数

② 用2，3，5，7去试除，有余数即为质数：

例：判断 77，87，97 这三个数是不是质数？

① 我们看：77÷7＝11 ，它是 7 的倍数，因此不是质数；② 再看 87 , 87÷3＝29 ，它是 3 的倍数，也不是质数。我们判断 87 是不是 3 的倍数，也可以用 8＋7 的和除以 3 ，这样也可以。③ 再看 97 ，它个位是 7 ，因此它不是 2 和 5 的倍数，下面就只需要判断 3 和 7 ，去除一下，就知道 97 也不是 3 和 7 的倍数，所以它是质数。

100以内的质数共有25个，这些质数我们经常用到，可以用下面的两种办法记住它们。

� 一、规律记忆法

� 首先记住2和3，而2和3两个质数的乘积为6。100以内的质数，一般都在6的倍数前、后的位置上。如5、7、11、13、19、23、29、31、37、41、43……只有25、35、49、55、65、77、85、91、95这几个6的倍数前后位置上的数不是质数，而这几个数都是5或7的倍数。由此可知：100以内6的倍数前、后位置上的两个数，只要不是5或7的倍数，就一定是质数。根据这个特点可以记住100以内的质数。

� 二、分类记忆法

� 我们可以把100以内的质数分为五类记忆。

�第一类：20以内的质数，共8个：2、3、5、7、11、13、17、19。

�第二类：个位数字是3或9，十位数字相差3的质数，共6个：23、29、53、59、83、89。

�第三类：个位数字是1或7，十位数字相差3的质数，共4个：31、37、61、67。

�第四类：个位数字是1、3或7，十位数字相差3的质数，共5个：41、43、47、71、73。

�第五类：还有2个持数是79和97。

� 一种简便的试商方法

� 试商是计算除数是三位数除法的关键，当除数接近整百数时，可以用“四舍五入法”来试商，然而当除数十位上是4、5、6不接近整百数时，试商就比较困难，有时需要多次调商。为了帮助同学们解决这个困难，下面介绍一种简便的试商方法。

� 当除数十位上是4时，舍去尾数看做整百数。用整百数做除数得出的商减1后去试商。

� 命名如1944÷243，除数十位上是4，把243看做200，1944÷200商9，用8(9－1)去试商正合适。

� 当除数十位上是5、6时，舍去尾数向百位进1，把除数看做整百数，用整百数做除数得出的商加1后去试商。

� 例如：1524÷254除数十位上是5，把254看做300，1524÷300商5，用6(5＋1)去试商正合适。

� 运用上面这种试商方法，有的可以直接得出准确商，有的只需调商一次就行了。同学们不试在计算除法时试一试。

100以内的质数表（25个）

2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，

67，71，73，79，83，89，97.

一到一百的质数有25个：2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97。 这些都是只能被他本身和1整除的数。

拓展资料：

质数又称素数，有无限个。质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数。否则称为合数。

质数的个数是无穷的。 欧几里得的《 几何原本》中有一个经典的证明。它使用了证明常用的方法： 反证法。具体证明如下：假设质数只有有限的n个，从小到大依次排列为p 1，p 2，……，p n，设N=p 1×p 2×……×p n，那么，p n加一是素数或者不是素数。

---