c42

c42 c42怎么算？

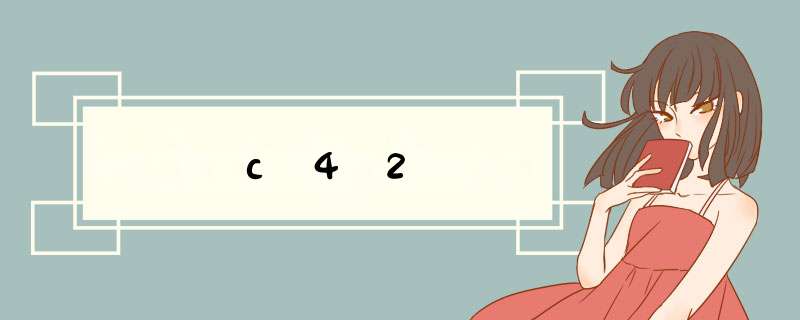
解题过程：C(4,2)=4!/(2!*2!)=(4*3)÷(2*1)=6组合C(n,m)=P(n,m)/P(m,m) =n!/m!（n-m）!；从n个不同元素中可重复地选取m个元素。

不管其顺序合成一组，当且仅当所取的元素相同，且同一元素所取的次数相同，则两个重复组合相同。

扩展资料排列组合计算方法如下：排列A(n，m)=n×（n-1）。

（n-m+1）=n!/（n-m）!(n为下标，m为上标，以下同)组合C(n，m)=P(n，m)/P(m，m) =n!/m!（n-m）!；例如：A(4，2)=4!/2!=4*3=12C(4，2)=4!/(2!*2!)=4*3/(2*1)=6

c42怎么算