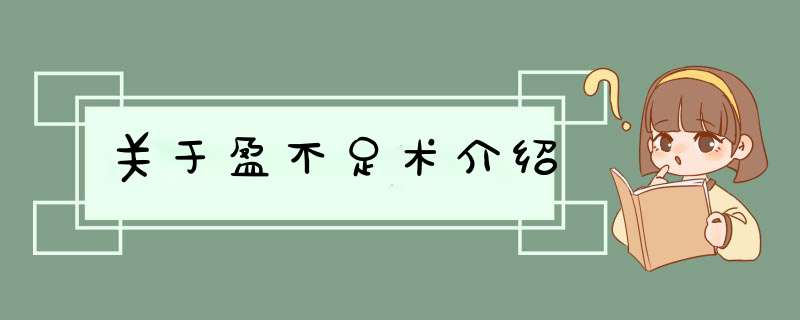
[拼音]:yingbuzushu
中国古代解决盈亏类问题的一种算术方法。成书于公元1世纪的中国古代数学名著《九章算术》 中,专辟一章名为“盈不足”。其中第一个问题是:“今有共买物,人出八,盈三;人出七,不足四。问人数、物价各几何?”这是有关盈不足术的典型问题,可用通用的数学符号表示如下:设每人出α1,盈(或不足)b)1,每人出α2,盈(或不足)b2,其中在“盈”时,b1,b2>0,“不足”时,b1,b2<0。《九章算术》给出了这个问题的一般解法,即平均每人应出钱数x,人数p和物价q,可分别用下列公式计算:
, (1)
, (2)
。 (3)
在上述问题中,由公式(2)(3)可得人数 p=7,物价q=53。盈不足术是中国数学史上的一项杰出成就。用盈不足算法不仅能解决盈亏类问题,而且能解决一些更复杂的问题。
在11~13世纪一些阿拉伯数学家的著作中,也出现了盈不足术,并称之为天秤术或契丹算法。当时阿拉伯人所说的“契丹”,即指中国。在欧洲中世纪,为了解决px-q=0这种类型的问题,有时用到所谓“双设法”,即通过两次假设以求未知数的方法。这种方法的大意是:设α1和α2是x的两个假设值,b1和b2是差值,这时有:
, (4)
。 (5)
(4)-(5),得,则。(4)·α2-(5)·α1,得,所以
,
于是
。
数学发展起来之前,双设法是中世纪欧洲解决算术问题的一种主要方法,并导致了正负号(+,-)的创用。当时这种方法还有许多别的名称,如双假位法或迭借术,增损术或盈朒术等。13世纪著名意大利数学家L.斐波那契在《算盘书》中说:“契丹法,阿拉伯名词。拉丁译文当为迭借法,……亦可称增损术。”明确指出了这种方法的渊源。因此,可以认为,正是中国古代的盈不足术经由阿拉伯传入欧洲,在欧洲数学发展中起了重要的作用。明代之后,中国传统数学逐渐失传,西方数学陆续传入中国。李之藻与利玛窦共同编译《同文算指》10卷(1613),载有双设法,译称“迭借互征”。于是,诞生于中国的盈不足术,经过一段漫长而曲折的道路,又重新回到了中国。
在现代数学中,求解线性方程已无需用盈不足术。但为计算高次数字方程或函数方程ƒ(x)=0的实根近似值,有时还要用到公式,显然此即公式(1)。在代数学和近似计算中,这种方法一般称为弦截法或线性插值法。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)