同余特性

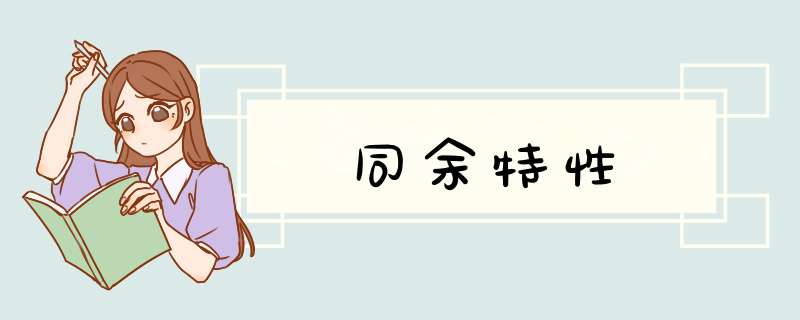
同余特性：1、对于同一个除数，两数的和（或差）于他们余数的和（或差）同余数。2、对于同一个除数，两数的乘积与他们余数的乘积同余。3、对于同一个除数，如果两个整数同余，那么他们的差就一定能被这个数整除。4、对于同一个除数，如果两个整数同余，那么他们的乘方仍然同余。

同余符号：

两个整数a、b，若它们除以整数m所得的余数相等，则称a与b对于模m同余或a同余于b模m。

记作：a≡b (mod m)，

读作：a同余于b模m，或读作a与b对模m同余，如26≡2(mod 12)。

定义：

设m是大于1的正整数，a、b是整数，如果m|(a-b)，则称a与b关于模m同余，记作a≡b(mod m)，读作a与b对模m同余。

显然，有如下事实：

1、若a≡0(mod m)，则m|a；