
译者注:以太坊网络是一台富状态(stateful)的世界计算机,其状态包括状态余额、交易流水号(nonce)、合约代码及合约存储内容等。在技术上,这些状态数据是靠一种叫做 “默克尔树” 的结构来组织的,因此,以太坊世界状态及其访问、更新,便可表达为一棵默克尔树及其访问、更新。同样地,所有跟默克尔树相关的数据证明及验证 *** 作,都可以在以太坊协议的语境下被理解为状态的证明及验证 *** 作。实际上,默克尔树是我们理解、利用、改进以太坊协议不可或缺的一环。本文介绍了一种可以证明多个值存在于同一棵默克尔树上的方法,因此也可以说,这就是在介绍如何证明多个以太坊状态隶属于同一时刻的世界状态的方法。
科普 | 什么是默克尔截顶
稀疏默克尔树多值证明(Sparse Merkle mulTIproofs)是对默克尔树截顶(Merkle pollard)的一种替代方案,可在为证明一棵默克尔树上存在多个值时提供空间上较为节约的证明。什么是默克尔证明、默克尔树截顶,我已在前一篇··文章中解释过了;推荐您先阅读并理解这些概念再来阅读本文。接下来,文本将用下图的默克尔树来解释多值证明:
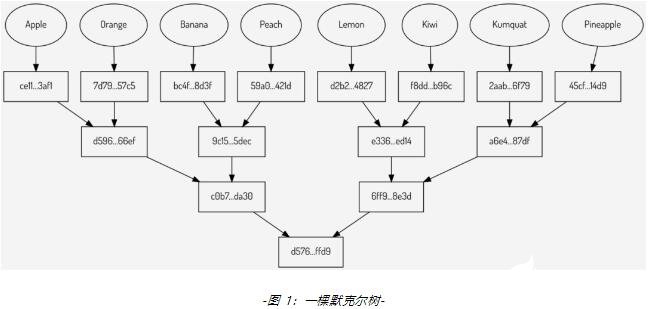
稀疏多值证明最早由 Vitalik Buterin 提出。
多值证明
多值证明(mulTIproof)就是把一棵默克尔树中的一组证明打包在一起,从而节省存储空间。例如,下面是上图所示默克尔树的 3 条默克尔证明:
从上图可以看出,3 个证明总共包含 9 个中间分支的哈希值(即由绿色标出的部分):每条证明有 3 个哈希值。将这 3 个证明组合成如下图所示的结构,即成多值证明:
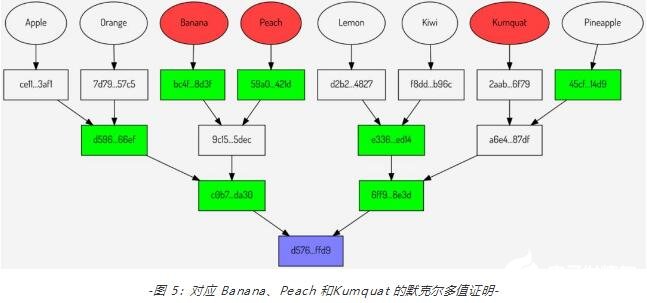
相比于单条证明时总共需要的 9 个中间分支哈希值,默克尔多值证明只需要 7 个哈希值,这就节省了存储空间。
稀疏的多值证明
虽然默克尔树的多值证明确实节省了一些存储空间,但其中一些数据可以用其他方式得到,所以移除这些数据可以进一步节省存储空间。(译者注:可通过其他方式得到的数据,就不需要存储在证明中,只要在需要时能够得到即可)
以上图的默克尔树多值证明为例,许多中间分支的哈希值都可以被计算出来。比如验证者将已知的值 Banana 和 Peach 通过哈希函数计算后,可以得到哈希值 bc4F…8d3f 和 59a0…421d。对于与根节点相连的两个节点的哈希值 c0b7…da30 和 6ff9…8e3d,可以通过其孩子节点(与两个节点直接相连的,并处于上方的节点)的哈希值计算出来。因为孩子节点的哈希值要么是证明中包含的,要么可以通过再上一层的哈希值计算出来。下图中黄色的节点标记了这 4 个可由计算得到的哈希值:
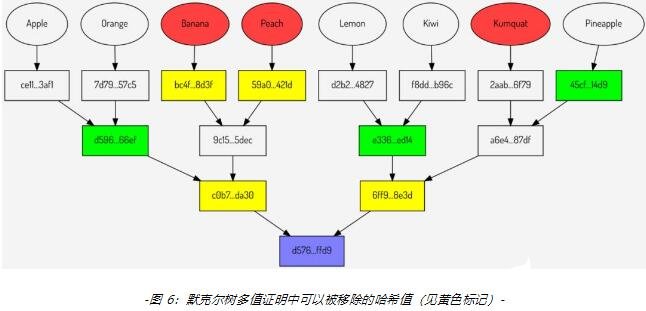
移除这些哈希值后,可以得到 默克尔树中稀疏的多值证明,如下图所示:
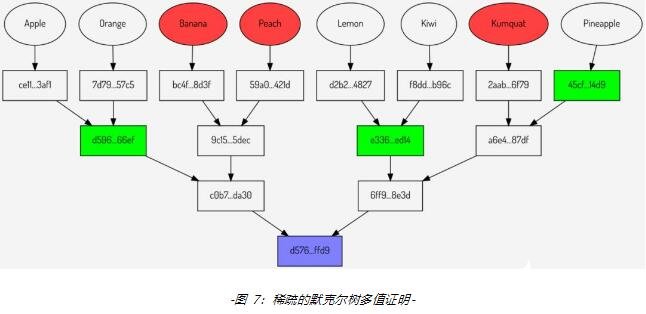
稀疏的默克尔树多值证明将需要包含的哈希值数量从 9 个减少到了 3 个。证明效果相同时,稀疏的多值证明也比默克尔截顶更有效,因为后者需要 6 个哈希值。
验证者得到稀疏的多值证明后,为了验证那些值是默克尔树的一部分,需要执行以下的步骤(在默克尔树中,依照从左到右,从上到下的顺序):
(译者注:“将某个值哈希”指:将值作为哈希函数的输入,得到随机的一串输出)
将 Banana 哈希得到 bc4f…8d3f
将Peach 哈希得到 59a0…421d
将 Kumquat 哈希得到 2aab…6f791
将bc4f…8d3f 和 59a0…421d哈希得到 9c15…5dec
将 2aab…6f79 和 45cf…14d9哈希得到 a6e4…87df
将d596…66ef 和 9c15…5dec 哈希得到 c0b7…da30
将e336…ed14 和 a6e4…87df 哈希得到 6ff9…8e3d
将c0b7…da30 和 6ff9…8e3d 哈希得到 d576…ffd9
至此可以把最终得到的哈希值与默克尔树的根哈希值做比较,如果二者一致,则认定所有的值都在该默克尔树中。
下图对比了默克尔树中值和证明的数量变化时,默克尔树截顶和默克尔树中稀疏的多值证明在存储默克尔证明时可以节约的空间存储量:
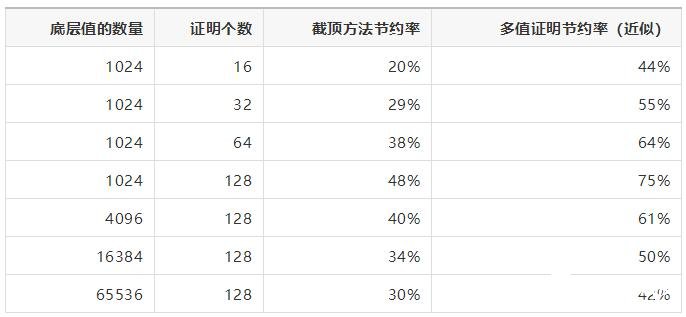
值得注意的是,多值证明的节省量是近似值,因为能节省多少取决于被证明的值在默克尔树中的位置以及可以被移除的中间分支哈希值个数。
对比稀疏多值证明与默克尔截顶
从上表中可以看出,稀疏的多值证明比默克尔树截顶节省更多的存储空间,那么为什么还要使用默克尔树截顶呢?因为稀疏的多值证明相对于默克尔树截顶,拥有一些不同的特性,主要有以下几点:
· 在多值证明方法中,所有值的证明都是一起生成、一起得到验证的;而在截顶方法中,各个值的证明是分别生成、分别验证的(译者注:生成及验证时,对截顶来说,具体是哪个值,只需要这个值和相关的证明即可,对于多值证明,则需要把要验证的多个值,以及多个值对应的证明都拿出来)
· 稀疏的多值证明在生成及验证证明时,需要更多的内存和 CPU 周期
· 稀疏的多值证明很难并行地生成和验证
· 稀疏的多值证明的大小是可变的,而默克尔树截顶在给定默克尔树和总证明数时,其证明大小是固定的
· 一些情况下,因为用于传输信息的编码系统不同,可能会导致稀疏的多值证明比默克尔树截顶需要更多的空间;因此建议使用之前做一下测试
总的来说,还要看单个应用的需求来决定哪个更合适。但是这两种方法都比单独的默克尔证明节省更多的存储空间,因此当需要对同一棵默克尔树提供多个证明时,可以考虑使用这两种方法。
责任编辑;zl
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)