基于TMS320C54X的RS+变织+卷积的级联纠错码_技术

随着越来越多的系统采用数字技术来实现，纠错编码技术也得到了越来越广泛的应用。如GSM标准中，对语音的信道编码采用卷积纠错、分组码检错。美国的蜂窝数字分组数据系统（CDPD）中采用了m=6的（63，47）RS(Reed Solomon)码。CDMA标准中，主要包括卷积编码（Turbo码等）、交织编码、帧循环校验等。DVD采用RS纠错编码。近些年来，随着软件无线电技术的发展，纠错编码一般都在通用的硬件平台上实现，这样有利于保证灵活性和通用性。通常采用基于FPGA的VHDL编码硬件实现，或者在DSP、单片机上用C和汇编编程软件实现。本文基于TMS320C54X的DSP，实现一种RS+交织+卷积的级联纠错码。

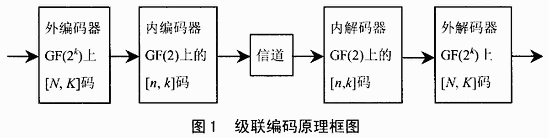
1 级联纠错编码原理

纠错编码技术是通过引入可控制的冗余来提高系统的可靠性。它的理论基石是1948年Shannon在《通信的数字理论》中提出的著名的有扰信道编码定理。纠错码按照不同的分类标准，有着不同的分类。我们常用的是按照对信息元处理的不同方法来分类的，分为分组码和卷积码。分组码是把信源输出的信息序列，以k个码元划分为一段，通过编码器把这段的k个信息元，按一定规则产生r个校验（监督）元，输出长为n=k+r的一个码组。比较常用的有BCH码、RS码、Hamming码等。卷积码是把输出信源输出的信息序列，以k0个（k0通常小于k）码元分为段，通过编码器输出长为n0(≥通常小于k)码元分为一段，通过编码器输出长为n0(≥通常小于k)码元分为一段，通过编码器输出为n0(≥k0)的一的码以。但是该码段的n0-k0个校验元不仅与本组的信息有关，而且也与其前m段信息元有关，称m为编码存储。因此卷积码用（n0，k0,k）表示。

由信道编码理论可知，随着码长n的增加，解码错误概率以指数方式趋近于零。因此，为提高纠错码的有效性，就必须使用长码。但码长增加，码率会相应下降，解码设备的复杂性与计算量也相应增加，级联码有针对性的解决这了一矛盾。它将编码过程分为前后串行的几级完成，可以满足信道纠错对编码长度的要求，得到与长码相同的纠错能力和高编码增益；而且增加的编/解码复杂度不是很大。其原理示意框图如图1所示。

级联码有内码和外码两级，内码是GF（2）上的一个[n,k]码，外码是GF（2k）上的[N,K]寿终正寝，编码规则如下。

①先将k×k个二进制信息元划分成K段，每段有k个信息元。

②每段的k个信息元可看成是GF（2k）上的一个符号。将K个符号按外码的编码规则编成一个外码，码长为N，有K个信息符号，N-K个校验符号，最小码距为do，码率Ro=K/N。

③外码的每一个符号，看成是k个二进制码元的码组，输入内码编码器，得到一个内存，码长n，有n-k个校验元，最小码距为di，码率Ri=k/n，由此得到N个[n,k]内码的码字序徇。两级编码总共得到N×n个二进制码元，K×k个信息元，组成[K×n，K×k，do×di]级联码的码。

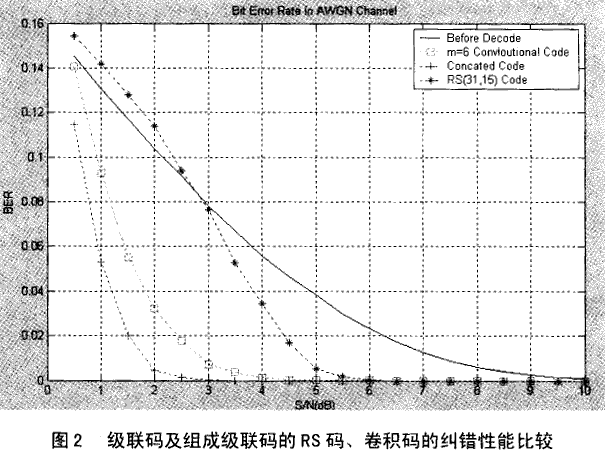
我们选用的外码为RS（31，15）码，生成多项式为G（X）=1+x2+x3，内码用卷积码（2，1，7），其生成多项式G0=171，G1=131（都是八进制）。RS码是GF（q）(q!=2)上，码长N=q-1的本原BCH码，具有很强的纠错能力，其最大可能的最小距离是校验元的个数加1，因而RS码是一种极大最小距离可分码（MDS），是一种最佳的线性循环码。本例中使用的RS（31，15）码的汉明距为17，可以纠8个错误。交织技术是抗突发干扰的重要手段，它是采用一个交织矩阵，存储方向与发送时的方向不一样，从而将突发错误离散化，提高抗突发干扰的能力。本方案中RS编码按行存储，发送时按列，并且对每列都进行卷积编码，可以抵抗8×列长的突发干扰。卷积编码Viterbi软判决解码，可以充分的利用各个码组之间的相关性，提高很高的编码增益。各个组成码和级联后的纠错性能仿真图如图2所示。

2 级联码的DSP编程实现

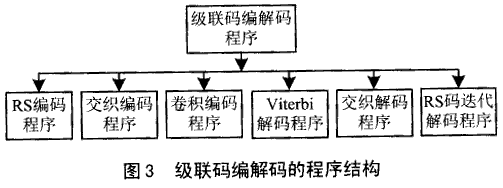
由于RS码和卷积码的Viterbi解码运算量都很大，所以需要大量的存储空间。本方案中实现在100kbps的信道上，RS码的解码运算量为8MIPS，Viterbi解码需要14MIPS。整个编解码程序需要24MIPS，因而选用在TMS320C54X芯片上实现。使用TI公司推出有XXA进行编程开发，考虑到编程的可移植性、可读性和效率，采用C语言与DSP汇编语言混合编程实现。Viterbi解码的算法由于程序运算量很大，采用DSP汇编语言来实现，蓁部分结构如图3所示。下面我们分别对整个系统中的关键部分RS码迭代解码和卷积码Viterbi解码中的编程进行阐述。

2.1 RS码迭代解码的实现

RS解码分频域解码和时域解码，比较常用的解码方法是时域的迭代解码。解码的主要步骤如下：①由接收码字r(x)求出部分伴随式Si的值，若Si全为0，则输出接收码字r(x)；②由伴随式Si求出σi(i=1,2,…K)，确定差错多项式σ（x）；③通过搜索法得到σ（x）的根，进一步确定差错位置βi；

④由部分伴随式Si及其差错位置βi求出差错大小；⑤由差错位置和差错大小求出误码多项式e(x)，计算c(x)=r(x)-e(x)；⑥校验是否成立，若成立，则输出c(x)，否则输出r(x)。

程序设计的关键在于域中运算的实现。对于中的乘法，可以采用指数形式表示元素，从而将相乘运算转换成相加运算。对于域中的加法，我们采用矢量形式表示，从而将加法运算转换成位异或运算。因而我们需要设计两张查找表，当遇到加法运算时，可以很方便的将元素从指数形式转换成矢量形式；遇到乘法时，可以将元素从矢量从指数形式转换成矢量形式；遇到乘法时，可以将元素从矢量形式转换成多项式形式。下面给出的是GF（2 4）域中，元素从指数形式转换矢量形式查表Alpha_to，由矢量形式转换成指数形式查表Index_of，其中域的生成多项式是g(x)=x5+x2+1。

Int Index_of[]={-1,31,1,18,2,5,19,11,3,29,6,27,20,8,12,23,4,10,30,17,7,22,28,26,21,25,9,16,13,14,24,15};

Int Alpha_to[]={1,2,4,8,16,5,10,20,13,26,17,7,14,28,29,31,27,19,3,6,12,24,21,15,30,25,23,11,22,9,18,1}；

由上面我们可以很方便地进行运算，例如伴随式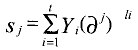的计算程序如下：

for(j=0;j

if(recd[j]!=0) s[i]^=Alpha_to[(Index_of[j])+i*j]]+i*j)%NN]；其中recd[]存储的是Yi的值。是域中的本原元。

2.2 卷积码Viterbi解码的实现

Viterbi解码算法是一种最大似然算法，它不是在网格图上依次比较所有可能的路径，而是接收一段，计算、比较一段，保留最有可能的路径，从而达到整个码序列是一个最大似然序列。虽然如此，Viterbi解码算法的运算量还是巨大的，而且随着卷积码结束长度的增大成几何级数增长。

2.2 卷积码Viterbi解码的实现

Viterbi解码算法是一种最大似然算法，它不是在网络图上依次比较所有可能的路径，而是接收一段，计算，比较一段，保留最有可能的路径，从而达到整个码序列是一个最大似然序列。虽然如此，Viterbi解码算法的运算量还是巨大的，而且随着卷积码约束长度的增大成几何级数增长。因而如何减少运算量，尽可能的采用结束长度长的码，成为Viterbi解码程序设计的关键。54X系列DSP中的结构和指令系统，通过精巧的算法和编程，可以使Viterbi解码快速实现。许多卷积码网络图中存在蝶形结构，因而可以利用DSP的相加、比较和存储单元（ACS）快速地实现蝶形运算。DSP的双字节指令，可以在个周期内进行单字节加减运算。指令系统包括单寻址重复和块指令重复 *** 作。总之，通过充分利用DSP芯片的特点进行编程，可以达到较快的速度。蝶形单元运算的宏编程如下：

BFLY_DIR .macro

DADST *AR5，A ；A=Old_Met（2*j）+T//Old_Met(2*j+1)-T

DSADT *AR5+,B ;B=Old_Met(2*j)-T//Old_Met(2*j+1)+T

CMPS A,*AR4+ ;New_Met(j)=(Max (Old_Met(2*j)+T,

;Old_Met(2*j+1)-T)TRN=TRN<<1

;If(Old_Met(2*j)+T=

;T)Then TRN[0]=1

CMPS B,*AR3+ ;New_Met(j+2^(k-2))=(Max(Old_Met

;(2*j)-T,Old_Met(2*j+1)+T)

;TRN=TRN<<1

;If(Old_Met(2*j)+T=

;T) Then TRN[0]=1

.endm

(2,1,7)的卷积码共有64个状态，需保留一条重量最大路径（幸存路径）。对每一个节点的组输入解码码元（2个），需要计算码元重量增量，通过32个蝶形运算单元来选择更新64个状态的存储路径。

由于解码处理的一个数据流，不可能等待所有输入完以后再解码，因而需要回溯。实验证明，当存储路径是约束长度的5倍时，每条路径的前端节点就收敛了，因而不需要等接收完成就可以输出。我们在编程中，采用了需要等接收完成就可以输出。我们在编程中，采用了固定长度的Viterbi解码算法，即一个帧长。因而在卷积码的编程器端需要添加0，使编码器的状态因而在卷积码的编码器端需要添加0，使编码器的状态最后归0。同样，在解码器端最后也是收敛于0状态。