整周模糊度的快速求解算法

整周模糊度的快速求解算法

1.1 备选整周模糊度解集的确定
利用GPS双差载波相位测量时，其数学模型为：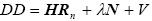

P0/0、X0/0初值的选取取决于对基线向量和初始模糊度范围的了解，基线分量及其变化速度分量初值可取为零，方差初值根据载体的动态情况选择，整周模糊度分量初值可取为伪距双差观测值，方差初值根据伪距的测量精度选择。
如果系统动态模型建立得比较准确(如静态时或载体运动规律已知时)，则当卡尔曼滤波器稳定后，整周模糊度估计值一般具有较高的精度，可以直接取与其最接近的整数作为整周模糊度，但一般需要较长的时间才能得到正确的模糊度，对于实时性要求较高的场合不适用。实际应用时一般是当Kalman滤波达到一定

图1 整数高斯变换前的置信椭圆 图2 整数高斯变换后的置信椭圆

为进一步减少备选整周模糊度组合，将所有的使用卫星分为两组：选4颗卫星作为主组，用来确定模糊度的搜索空间，其余卫星作为从组，用于模糊度的检验。
对选为主组的4颗卫星，取其双差模糊度的浮点估计值及其方差阵进行高斯变换，得变换后的模糊度估，将对主组双差模糊度按式(16)确定的置信空间中的所有组合作为备选整周模糊度解集。