实时T-S型模糊控制器设计及其在CAN总线控制系统中的应用

摘 要： 本文提出了一种实时模糊控制算法，并应用到基于CAN总线的运动控制系统中，且给出了系统的整体结构和现场控制单元的设计方案。实验结果表明，该控制系统具有实时性强、响应速度快、精度高的特点，在现场控制中有效可行。

引言
随着模糊控制理论的发展，Takagi-Sugeno模型(简称T-S模型)的出现将模糊控制的研究推向了一个高潮。实践证明，具有线性后件的T-S模糊模型以模糊IF~THEN规则的形式充分利用系统局部信息和专家控制经验，可以任意精度逼近实际被控对象。但是，由于T-S模型以及相应模糊控制器的建立需要确定较多的参数且推理复杂，使得该模型仅用于理论分析，实际使用的T-S型模糊控制器至今未见报道。现场总线技术的兴起，改变了传统控制系统的结构，形成了控制网络。由于其适应了控制系统向智能化、网络化、分散化发展的趋势，因而显示出强大的生命力，成为控制领域的热点技术。
基于上述考虑，本文通过对T-S模型推理过程的简化得到了一种实用的模糊控制算法，并将该算法与现场总线技术有机地结合起来，实现了基于CAN总线的实时模糊运动控制系统。

模糊控制器的设计
对于复杂被控对象而言，在系统局部信息或专家控制经验可得到的情况下，通过系统辨识、经验归纳等方法得到多条规则作为T-S型模糊控制系统的参考规则库。对于任意实时输入，利用模糊模式识别技术在规则库中寻找一条与该输入最匹配的规则(控制规则中心)，并以之为基础，对整个参考规则库进行动态简化，从而得到控制量。其模糊控制系统如图1所示。

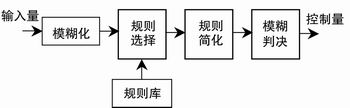
图1 规则简化的模糊控制系统

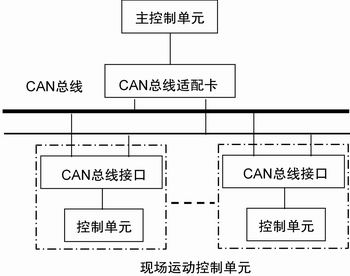
图2 基于CAN总线的模糊运动控制系统

对于给定被控对象，考虑如下一组模糊参考规则：
(1)
其中，为输入语言变量；是第i条参考规则中与前件输入变量对应的语言变量值；为后件输出量，是第i条规则的后件系数。将参考规则中的前件语言真值转换为对应论域中的模糊数形式，则上述条规则可写成如下矩阵形式：

其中，L是用模糊数表示的规则前件语言值；P是规则的后件系数阵；X、Y分别是输入和输出向量。
假设在任意采样时刻K，系统实时输入精确量为Xk=(x1k x2k L xnk)，经过模糊化，按照最大隶属度原则，可得到一组输入语言值XkL=(L1k L2k L Lnk)等价的模糊数形式为
XkL=(l1k l2k L lnk) (2)
下面，将从参考规则库中寻找与该输入组合最接近的规则，也即“控制规则中心”。
把矩阵写成行向量的形式，即
L=(L1 L2 L Lm)T (3)
其中，Li=(li1 li2 L lin)称为模糊模式。这样，L矩阵确定了m个模糊模式。需要强调一点，m个模式应覆盖整个系统的输入输出空间，也即模糊模型应该是完备的。
计算(3)式与每一模糊模式L之间的Euclid距离及最大Euclid距离，
(4)
采用最大隶属度原则，即可求得“控制规则中心”；也就是说，如果存在mLa(XkL)=max[mL1(XkL), mL2(XkL), L , mLm(XkL)]则认为实时输入XkL优先隶属于La模式，可得“控制规则中心”为Ra。其中，
为实时输入关于模糊模式的隶属度。
以规则Ra为基础，可将参考规则库简化为

其中，b1,b2,L,bm为适当的后件比例系数。
考虑到实际输入XkL与各模糊模式之间的差别，取，利用重心法解模糊，可得控制器的输出为
(5)
其中，为第i条规则的前件强度。
上述简化T-S型模糊控制器处理方法的优点在于：
(1)突出了“控制规则中心”在整个控制器输出中的基础性作用，使得控制更符合专家经验。
(2)选用作为简化规则的后件比例系数，充分考虑了输入组合与各模糊模式之间的不完全一致性。
(3)在线推理和运算工作量的减少，使控制器的实时性得到了提高。
需要注意的是，在(5)式中，变量系数会随着实时输入的变化而变化，原因在于不同的输入对应着不同的“控制规则中心”。因此，从整体来看，该模糊控制器又是一个变结构的控制器。

基于CAN总线的运动控制系统的实现
在雕刻机、数控机床、电动叉车、柔性制造系统等应用场合，往往要求各个电机能够在不同条件下以不同的速度协调运行，分别实现不同精度的定位等功能，目前多采用集中控制方式，但是，其存在响应速度慢、抗干扰能力差、对数据通信可靠性要求高等固有缺点。同时，现有控制器一般采用单片机、86系列微控制器等作为硬件核心，尽管价格便宜，但由于运算速度和存储容量的限制，一般适用于简单控制过程和“慢”过程，在一些加工工艺复杂、动作协调要求高的场合，其应用十分有限。 本文设计了以CAN总线为基础，以数字信号处理器为硬件平台的模糊运动控制系统，能很好解决这一问题，其结构框图如图2所示。
硬件结构
在一些多电机或多轴运动控制系统中，每个电机或轴的位置、速度等都必须单独地受一个更高级别的控制器控制，且同一个过程单元中的几个电机之间可能也需要传递一些实时数据。因此，可以通过CAN总线将多个独立的现场运动控制器和主控制器互连起来，主控制器在一个更高的层次上，向各个电机发送参考运动信息(设定位置、速度，力矩等)，并且等待来自测量器件的反馈。同时，各运动控制器之间也可以交换必要的数据信息。实现上述功能的硬件结构如图3所示。
现场运动控制单元以TI公司的TMS320LF2407A数字信号处理器芯片为硬件核心，它主要负责现场数据的采集和处理，以及通过CAN总线收发器与其它现场控制单元及主控制器之间的通信；TPIC82501为CAN总线收发器，符合CAN2.0B标准，主要负责把TMS320LF2407A发出的信息转换为CAN协议格式，且将之发送到CAN总线上供主控制器和其它控制单元使用，同时，接收从CAN总线上来的数据供TMS320LF2407A做进一步的处理；IR2103S、IR2144和大功率MOSFET管，共同构成电机的驱动电路。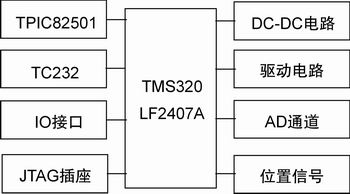

图3 现场运动控制单元

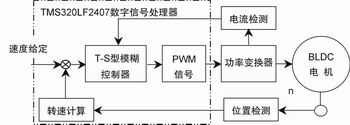
图4 无刷直流电机的转速控制系统

软件结构
在现场运动控制单元中，初始化程序和模糊控制算法实现程序分别采用TMS320LF2407A的汇编语言和C语言编制。电流检测、位置检测、PWM输出都采用中断方式来实现；运行速度、位置等参考值由主控制器、上位机或其它现场单元提供，通过电路板上的CAN收发器输入LF2407A；电机的运行速度、相电流、轴位置等信息分别通过LF2407A的捕获单元、片上A/D转换器、正交脉冲编码电路等得到；对电机的控制通过LF2407A的事件管理器模块EVA、EVB输出具有适当占空比的PWM脉冲给大功率MOSFET管来实现。

运行结果
为验证本文算法的有效性，我们设计了以CAN总线为基础、TMS320LF2407A数字信号处理器为核心的三相无刷直流电机的速度控制系统，如图4所示。参考速度由主控制器通过CAN总线输入，系统采用电压PWM调制策略。
图中三相无刷直流电机的定子绕组为三相星形、定子每相感抗为40mH、相阻抗为190mΩ、在5000rpm时，最大允许电流是4.3A、转矩常数为17.2mNm/A。采用本文介绍的控制系统，当负载转矩从减少为；设定转速为800rpm和400rpm时，转速波形分别达到了预定的要求。虽然本文控制器采用了实时模糊推理，增加了计算量，但是，由于使用了简化T-S模型和数字信号处理器作为软件和硬件基础，保证了实时性和较高的控制精度。

结语
本文对T-S模糊模型进行了研究，着眼于控制系统综合的容易实现、快速响应、实时性等指标，通过对模型进行合理简化，得到了一种实时模糊控制算法，同时，针对目前广泛使用的多轴运动控制系统的特点进行了分析，介绍了一种采用CAN总线实现多电机运动控制的分布式智能系统。实验结果表明，所得到的基于CAN总线的模糊控制器具有较高的精确度，较好的实时性和动特性。