基于FPGA技术的全方位移动机器人运动控制系统的方案设计

　　0 引言

　　目前，全方位移动机器人由于具有出色的灵活性，已经成为RoboCup中型组足球机器人比赛中最理想的选择。而机器人的运动控制一直以来都是直接影响机器人性能的主要因素，也是移动机器人研究的热点之一。本文研究了一种用FPGA技术实现三轮全方位移动机器人运动控制系统的方法，与双DSP结构，DSP+CPLD结构，以及DSP+专用集成电路结构等相比，该方法具有简单可靠，扩展性强等特点。且FPGA设计简单，使用方便，开发周期短，能够实现真正的SOPC系统。

　　1 全方位移动机器人运动模型

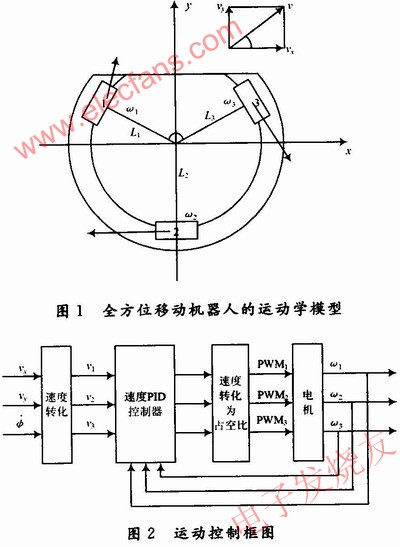
　　设世界坐标系下机器人的速度为ε=[vx，vy，φ]，则当vx=O，vy≠0，φ=O时，机器人做前后方向的直线运动，当vx≠0，vy=0，φ=0时，机器人做左右方向的直线运动，当vx=0，vy=0，φ≠0时，机器人做自转运动。图1中，ω1，ω2，ω3为3个主动轮的转动角速度，R为全向轮半径;L1，L2，L3为机器人车体中心到3组全向轮中心的水平距离，设有L1=L2=L3=L。α为前两轮之间的夹角，另外2个夹角均为180°-α/2。则机器人坐标系下的速度到三轮速度之间的关系如下：

　　

　　

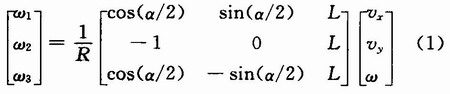
　　由式(1)可以看到：知道了机器人在平面世界坐标系中的速度要求后，便可以得到主动轮的速度要求，进而对电机发出相应的控制信号。

　　2运动控制方案本系统总体设计思路如图2所示，首先通过RS 232接口，实现PC机与底层控制芯片FPGA的通信，FPGA在接收到相关的机器人坐标系下的速度后，将机器人坐标系下的速度值转化成机器人3个全向轮子的角速度，将得到的角速度值计算出相应的占空比，生成相应占空比的PWM波形，输出信号接到直流伺服电机驱动器，然后通过FPGA采集正交编码盘信号，计算出轮子实际的角速度值，做PID速度闭环控制。鉴于FPGA模块复制的优势，这里对每个全向轮分别做了PID闭环控制。

　　3 系统硬件设计

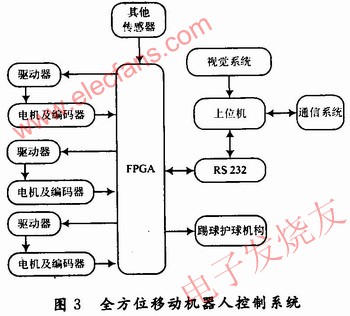
　　采用的三轮全方位移动机器人系统框图如图3所示，上位机主要完成图像信息的采集、处理、路径规划，并实现与场外裁判盒的通信。下位机主要是FPGA，主要实现三轮编码信号的采集，PID速度闭环控制，踢球控制，电机控制信号的产生，还有其他的传感器信息的采集等，并负责与上位机之间的信息交互。本设计只是完成了下位机运动控制部分。

　　

　　3.1 正交编码信号采集与测速实现

　　增量式光电编码器输出信号如图4所示。

　　

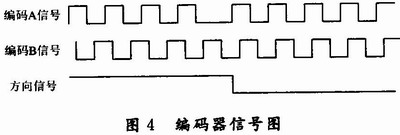
　　A、B两相信号是相位相差90°的正交方波脉冲串，每个脉冲代表被测对象旋转了一定的角度，A、B之间的相位关系则反映了被测对象的旋转方向。在FPGA中设计4倍频和鉴向电路，本设计采用2路输出：一路输出方向，另一路输出脉冲，并对鉴向倍频电路进行仿真，如图5所示。

　　

　　根据脉冲计数来测量转速的方法有M法、T法以及M/T法3种。M法适用于高速测量场合，在低速时有较大的误差;而T法，恰恰相反，在低速时测量准确，高速时误差较大。

　　

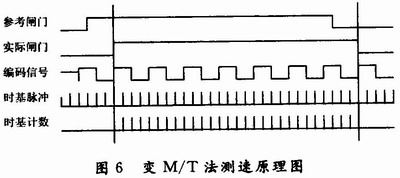
　　本设计采用文献所描述的方法。该方法如图6所示，设定参考闸门时间为固定的1个值，它只是作为参考信号和编码信号共同确定实际的闸门时间。这样确定的闸门时间为被测信号的整周期倍，能够有效提高测量精度。则测得的速度为：

　　

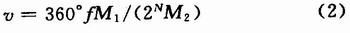
　　4. 增量式PID控制原理及其FPGA实现

　　实际机器人的数学模型不可避免地存在一定程度的参数不确定性，且三轮全方位移动机器人的正交全向轮在行走时会与地面交替接触而产生一些不确定摩擦转矩，这些都会给机器人的精确控制带来难度。为了对三轮全方位移动机器人进行精确的控制，系统采用PID速度闭环控制算法对机器人的3个全向轮进行速度调节。

　　令采样周期为TS，将连续PID公式离散化后可得到数字PID算法表达式：

　　

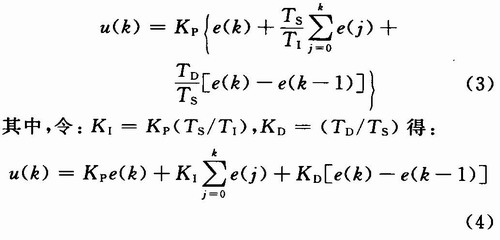
　　式中：k为采样序号;u(k)为第k个采样时刻的计算机输出值;e(k)为第k个采样时刻的计算机输入误差值;e(k-1)为第k-1个采样时刻的输入误差值;Kp为比例系数;KI为积分系数;KD为微分系数。

　　这种算法虽然比较直观，但由于是全量输出，所以每次输出均与过去的所有状态有关，计算时要对e(k)进行累加，计算机运算量大。

　　于是产生了增量式PID算法：

　　

　　

　　

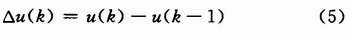
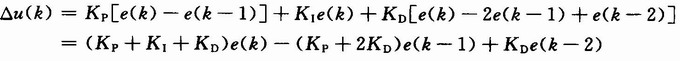
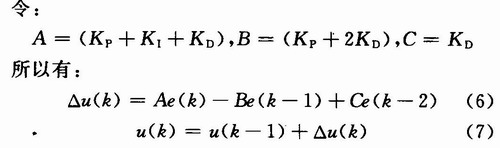
　　上述公式(7)为增量式PID控制算法。只输出控制增量，误动作影响较小，且控制增量只与最近几次的采样值有关，容易通过加权处理获得比较好的控制效果。

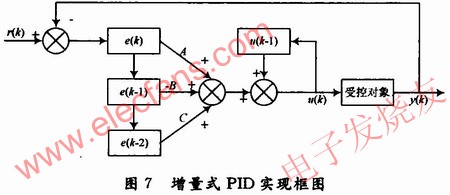
　　根据以上公式推导，结合FPGA的工作特点，本文设计了适合FPGA的增量式PID实现结构。

　　由图7可以看出，增量式PID控制算法程序结构，只要最近的3个误差采样值就可以加权计算。这在FPGA内部完全可以并行实现，移位部分结构类似FIR滤波器的实现结构，难点是FPGA设计时对有符号数的熟练 *** 作和保证累加器不能溢出。

　　

　　一种高效的硬件测试手段和系统测试方法，它能够获取并显示可编程片上系统(SOPC)的实时信号，它可以随设计文件一起下载到FPGA中，用于捕捉FPGA内部节点和I/0引脚的状态，就如同使用真的逻辑分析仪一样，对设计进行在线仿真，但又不影响硬件系统的工作。为了检验测得的全向轮实际速度值是否准确，对设计的测速模块进行了在线仿真。设定每个全向轮以固定的速度转动，对比测得的实际速度值和设定的速度值，如图8所示。

　　

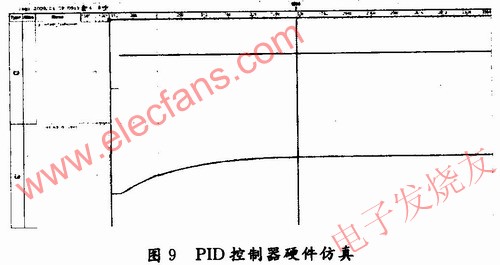
　　在嵌入式逻辑分析仪中，对PID模块也进行了在线测试。实验条件：在空载条件下，频繁变化电机的速度，通过嵌入式逻辑分析仪观察FPGA内部PID调节后的速度值和设定值，图9所示为一号全向轮的速度设定值与反馈速度值。

　　

　　三轮全方位移动机器人与双轮差速不同，具有很大的灵活性，况且由于3个全向轮的负载的不同，使得机器人不能走出精确的直线。而要实现机器人的精确控制，一个前提就是让它能够走出很直的直线。为检验机器人控制性能，设计了如下实验：机器人以固定速度分别向前后左右4个方向行走，先观察没有加入PID控制算法时的情况，然后再观察加入PID控制算法时的情况。实验的结果如表1所示。

　　

　　分析：由于机器人的3个全向轮所承受的负载不一样，即在相同的占空比的PWM下，3个轮子的实际速度并不相同，这就使得三轮速度不可能准确合成机器人的速度，进而影响机器人的控制轨迹。根据图1所示的机器人1号轮和3号轮负载相当，2号轮子承受的负载较大，没有加入PID控制器时，前后运动虽然在一定范围内近似直线，但是机器人运行的速度达不到预期设定的速度，左右运动轨迹就是一个圆，而且设定的机器人左右移动速度大小还决定了机器人是朝顺时针方向还是逆时针方向转圈。加入PID控制算法后，轮子的速度得到校正，机器人能够以预期设定的速度前后左右运动，特别是左右运动在一定范围内近似为直线，不再是圆圈。可见PID闭环控制算法明显提高了机器人的控制性能。

　　5 结语

　　针对目前常见的以DSP为核心实现足球机器人底层运动控制系统的方案，提出了一种采用FPGA实现三轮全方位移动足球机器人的底层运动控制系统的方法。通过在三轮足球机器人上的应用实践，发现这种采用FPGA实现的方案有很好的实时性，精确度较高，而且由于FPGA本身的引脚多特点，其可扩展性较强，比如可以通过串口配置数字罗盘等外围信息传感器等其他传感器，同时，本设计对于研究多电机的机器人运动控制系统的实现方案有重要的参考价值和实用价值。

　　另外，由于全向轮的随动性较强，且易打滑，在实行精确控制的时候方向容易受到影响，而且PID闭环控制算法反应时间较长，参数还需要更多时间的调试，在以后的研究中，我们将研究更为精确的控制算法，实现对机器人的精确控制。

欢迎转载，本文来自电子发烧友网(http://www.elecfans.com/)