遇到不会的运放电路怎么办？

　　在此特别鸣谢 公众号《硬件笔记本》

运放电路总是五花八门，让人眼花缭乱。有时候遇到一个复杂的运放电路，看着都头大，让人无从下手。其实再复杂的电路都是由简单的电路演变而来的，都是有方法的。

分析运放最常用的方法就是“虚短”和“虚断”。毕竟实际工作中很多电路都不能直接套公式，懂得计算才是王道。

下面是我算的部分草稿（还是比较用心了，字写的比较丑，别见笑）

“虚短”是指在分析运放处于线性状态时，可以把两输入端视为相同电位，这一特性称为虚假短路，简称虚短。

“虚断”是指在分析运放处于线性状态时，可以把两输入端视为等效断开，这一特性称为虚假开路，简称虚断。

下列是常用的几种运放电路

同相运算电路

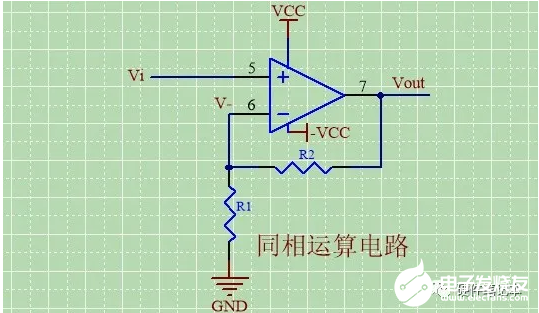
由虚短，得Vi=V-；

由虚断，得R1，R2可近似看成串联，则流经R1，R2的电流相等，即IR1=IR2；

（Vout-V-）/R2=V-/R1；

即（Vout-Vi）/R2=Vi/R1；

故Vout=Vi*（R2/R1）+Vi=Vi（R2/R1+1）；

反相运算电路

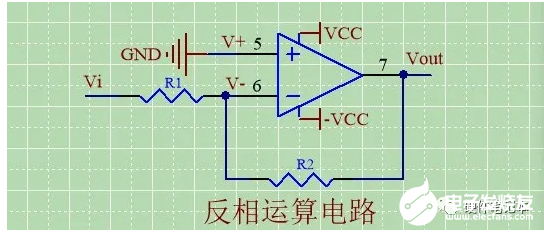
由虚短，得V-=V+=0；

因此，流经R1电流IR1=（Vi-V-）/R1=Vi/R1；……①

由虚断，得

得IR1=IR2；……②

因此IR2=（-Vout）/R2；……③

根据①②③得：Vout=-Vi*（R2/R1）

加法运算电路1

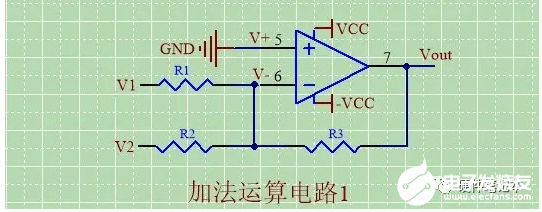
由虚短，得V-=V+=0；

由虚断，得流经R1，R2和R3电流分别为

IR1=V1/R1；

IR2=V2/R2；

IR3=-Vout/R3；

根据基尔霍夫电流定律，可知流经R3的电流等于IR1+IR2；

即IR3=IR1+IR2；

即-Vout/R3=V1/R1+V2/R2；

若R1，R2，R3的值相同，

则Vout=-（V1+V2）；

加法运算电路2

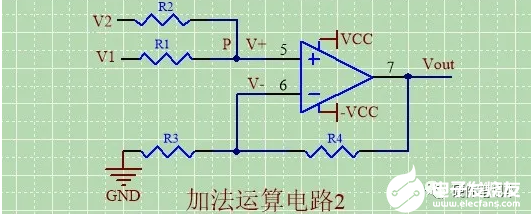
由虚断，得R3，R4串联，流过电流相等；

即IR3=IR4；

即（V-） /R3={Vout-（V-）}/R4；

即Vout=（1+R4/R3）*（V-）；

由虚断（运放输入阻抗无穷大），得节点P的电流方程

IR1+IR2=0，

即{V1-（V+）}/R1+{V2-（V+）}/R2=0；

化简得（V+）=（V1*R2+V2*R1）/（R1+R2）；

由虚短，得V-=V+；

所以Vout=（1+R4/R3）*（V1*R2+V2*R1）/（R1+R2）

若R1=R2，R3=R4，

则Vout=V1+V2；

减法运算电路

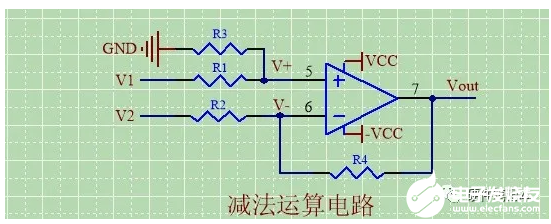
由虚断，得R1和R3，R2和R4可近似看成串联，则流经其电阻电流

IR1=IR3；IR2=IR4；

即{V1-（V+）}/R1=（V+）/R3；……①

{V2-（V-）}/R2={（V-）-Vout}/R4；……②

由虚短得，V-=V+；……③

由①②③得

Vout=（R2+R4）/（R1+R3）*R3/R2*V1-R4/R2*V2

若R1=R2=R3=R4，

则Vout=V1-V2；

积分运算电路

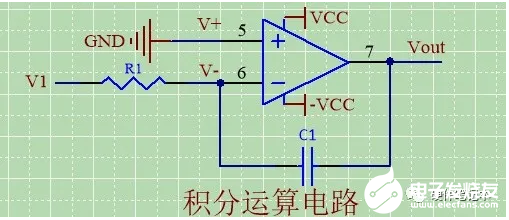
由虚短，得V+=V-=0；

由虚断，得IR1=IC1；

又IR1={V1-（V-）}/R1=V1/R1；

又IC1=C1*d（VC1）/dt=-C1*d（Vout）/dt；

化简得Vout={（-1/（R1*C1）}∫V1dt

微分运算电路

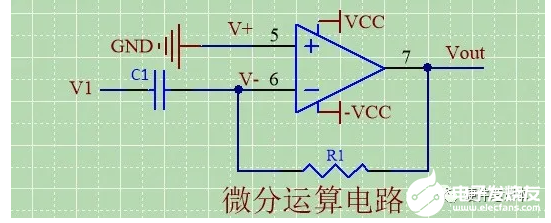
由虚短，得V+=V-=0；

由虚断，得IC1=IR1；

又IC1=C1*d（VC1）/dt=C1*d（V1）/dt；

又IR1=（V1-Vout）/R1=（-Vout）/R1；

化简得Vout= -（d（V1）/dt*C1*R1）