
随着集成电路技术的不断进步,数字化应用逐渐普及,在数字通信、电力系统自动化等方面越来越多地运用了数字锁相环。它的好处在于免去了模拟器件的繁琐,而且成本低、易实现、省资源。本文综合以上考虑,在一片FPGA中以Quartus II为平台用VHDL实现了一个全数字锁相环功能模块,构成了片内锁相环。
数字锁相环是一种相位反馈控制系统。在数字锁相环中,由于误差控制信号是离散的数字信号而不是模拟信号,与之相对应,受控的输出相位的改变是离散的而不是连续的;此外,环路组成的部件也全由数字电路实现,故名“数字锁相环”。常用的数字锁相环原理如图1所示。
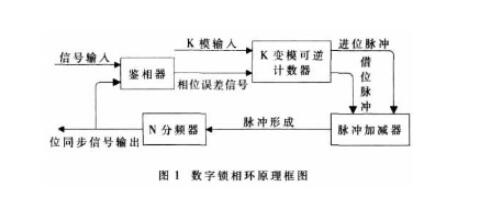
1 数字锁相环的结构及工作原理
如图1所示,数字锁相环主要由鉴相器、K变模可逆计数器、脉冲加减器、N分频器构成。
鉴相器其实就是一个异或门,它将输入信号Din与位同步脉冲输出信号Dout相异或,比较它们之间的相位差,并输出相位误差信号作为K变模可逆计数器的计数方向的控制信号CS。当环路锁定时,这个控制信号为占空比是50%的方波。
K变模可逆计数器根据相差信号CS的变化,向不同的方向计数。当CS为逻辑“1”时,计数器向下计数,如果计到0,则输出一个借位脉冲给脉冲加减器;当CS为逻辑“0”时,计数器向上计数,如果计到模值,则输出一个进位脉冲给脉冲加减器。
脉冲加减器是根据K变模可逆计数器输出的进位、借位脉冲来不断地对本地时钟进行调整。当有进位脉冲时,脉冲加减器就在本地时钟上加入一个周期的时钟信号;当有借位脉冲时,脉冲加减器就在本地时钟上扣除一个周期的时钟信号。如此反复不断地对本地时钟进行调整,最终达到准确确定出输入信号时钟的目的,从而实现位同步[2]。
N分频器是将脉冲加减器输出的经过调整以后的时钟信号进行分频,以减小同步误差。N值越大得到的同步误差越小。
2 数字锁相环各部分的VHDL实现
K变模可逆计数器根据预设模值Kmode来设置对应的模值寄存器的值,也即当预设模值范围在0~15变化时,与之相对应的Ktop的变化范围为20~215。模值的大小直接决定了数字锁相环锁定时间的长短,模值越大锁定时间越长,反之越小。但锁定时间越长,锁定时的相位误差越小,反之越大。这部分的VHDL设计程序[3]如下:

有了K变模可逆计数器产生的进位、借位脉冲,脉冲加减器就可以按照这两种脉冲对本地高频时钟进行不断地调整,如图2所示。
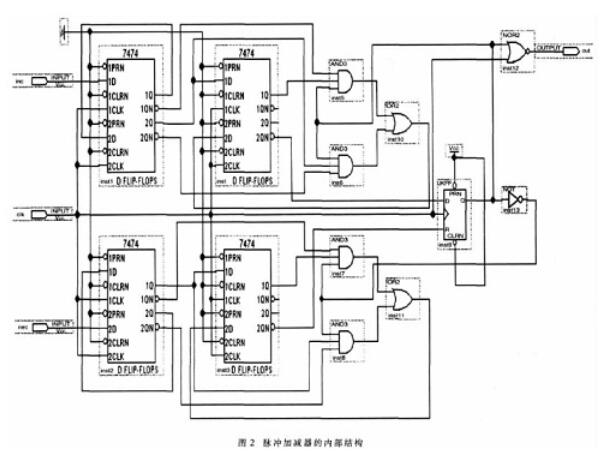
N分频器的设计相对简单,其功能是将脉冲加减器输出的经过了调整的本地时钟进行N分频,以减小同步脉冲输出误差。本例暂时用32分频代替,其VHDL设计程序如下:

按照图1数字锁相环原理框图的设计理念,设计出各个主要的功能块,并将它们各自进行仿真。在确认无误后再连接起来进行综合仿真,以验证设计的正确性。在综合仿真的过程中一个最关键的问题就是分析各个功能块的时序关系、频率关系。
3 频率关系、时序分析
假设输入信号的频率为fi=1 200 Hz,则位同步输出信号频率fo=1 200 Hz,脉冲加减器输出信号频率fm2=N×fo,则其时钟频率fm1=2×fm2;K变模可逆计数器工作时钟可设为M fo。这里的M、N值一般均为2的整数次幂,他们之间的具体关系需根据fi确定。综合仿真的时序图如图3所示。
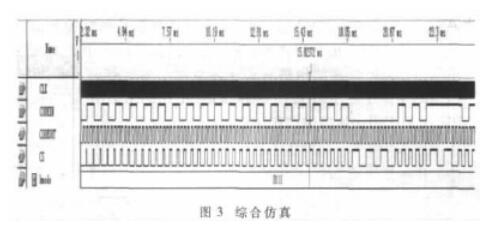
由图3可以看出,CS控制信号逐渐变成了占空比为50%的方波,这也从侧面反映出了锁定过程。当锁相环锁定后,信号CODEIN出现连“0”和连“1”时,也能准确实现位同步。锁定时间约为15.8 ms。通过以上仿真,验证了设计的正确性。对于不同的设计,只需要计算好频率关系、修改一下N分频器的N值,就可以实现不同输入信号的同步。
本文介绍的这种以VHDL语言实现的全数字锁相环,是在ALTERA公司的Cyclone系列FPGA—EP1C12Q240C8上实现的。它仅仅需要FPGA的95个逻辑单元,对于拥有12 060个逻辑单元的EP1C12来说,消耗的资源微乎其微,但却是信号的差分相干解调过程中不可或缺的重要部分。通过以上方法介绍、仿真的实现,再一次体现了用硬件描述语言在可编程器件中实现数字电路的优越性。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)