二阶有源滤波器的传输函数

二阶有源滤波器的传输函数

在有源滤波器的设计中，高阶滤波器的传输函数都可以分解成一阶和多个二阶传输函数的乘积。一阶传输函数比较简单，二阶函数分析如下。

1、低通滤波器

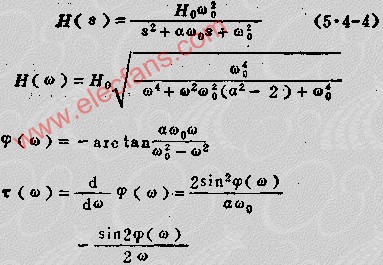
2、高通滤波器

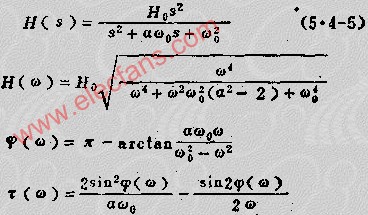
式中，HO为传输增益双称通频带增益：A为阻尼系数，WO为滤波器的固有频率，S=JW。

幅频特性H（W）、相频特性φ（W）和延迟特性T（W）表示了低、高通滤波器的全部特性。H（S）是传输函数。

由图5.4-47可以看出，A取值不同，曲线的形状可以有很大不同，也就是对滤波器的滤波性能有很大影响。当A=√2时，幅频响应有最大平坦区，是巴特沃斯滤波器；A﹤√2时，在WO附近有凸峰；通带内有等值波动。A值越小，阻尼越小，凸峰越明显，通带内幅度等值波动越大，选择性越好。是切比雪夫滤波器。A值越大，阻尼越大，曲线变化趋于缓慢。当A=√3时，幅频响应平坦区较小，具有线性相移的特性，是贝塞尔滤波器。

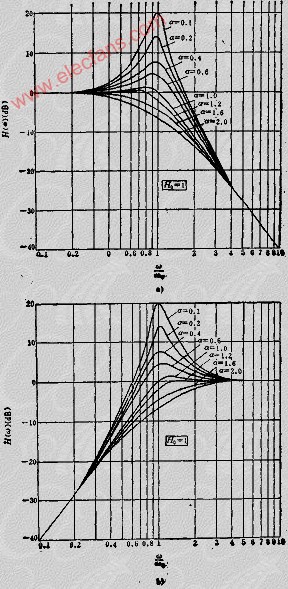
图5.4-47 幅频特性曲线
A）低通滤波器具  B）高通滤波器

3、带通滤波器

4、带阻滤波器

式中 Q为品质因数（选择性因子）；W为通带中心频率；BW为滤波器带宽；W2为高端截止频率；W1为低端截止频率。

由图5.4-48可以看出，W值愈高，曲线愈陡，通频带越窄，选频特性越好。Q值愈低，曲线变化迟缓，通频带越宽，选频特性越差。Q与A的关系为：Q=1/a

图5.4-48 幅频特性曲线
A）带通滤波器  B）带阻滤波器

本文地址：https://www.elecfans.com/arTIcle/analog/2010/20100523218383.html