有源视频滤波器

摘要：最初，视频滤波器是一个无源的LC电路，周围是放大器。现在将放大器与RC滤波器结合起来，可以获得尺寸更小、效率更高的设计，此外，二十世纪60年代发展起来的灵敏度分析与预失真方法也克服了早期滤波器性能较差的弱点。

高性能运放和PC上的专用软件方便了宽带有源滤波器的设计，但这并未解决任意特定应用的问题。对视频滤波器而言，特定的应用与信号制式给每个电路设计都带来了细微的差别。以下是两类主要的视频应用。

抗混叠滤波器：这一类器件被放置在模数转换器(ADC)之前，用来衰减信号中Nyquist频率以上的成分，即高于ADC采样率一半的信号分量。这些滤波器的响应通常都设计得尽可能陡，目的是尽可能将截止频率¹以上的信号统统滤掉。对ITU-601以及其他应用来说，这样的性能是通过将模拟滤波器、数字滤波器以及过采样ADC结合运用来实现的。而对PC图像之类的应用，少量的滤波就足够了。

重建滤波器：也被称作(sinx)/x或零阶保持校正器，这类器件被放置在数模转换器(DAC)之后，用来消除由采样带来的多重映像，并不是为了消除DAC时钟串扰。重建滤波器很少有象抗混叠滤波器那样的选择性，因为DAC的保持功能也有滤波的作用—这种作用降低了对选择性的要求，但给响应带来了损失。现有的视频信号制式包括RGB、分量视频、复合视频和RGB PC图像等。

所有应用与制式都希望视频滤波器能做到“相位线性”，这是群延时(不同频率的延时)特性所要求的。所需的相位线性度取决于具体的应用与视频制式。例如，抗混叠滤波器与分量制式比重建应用与复合视频的要求更严格。各种应用与制式的要求由NTSC、PAL/DVB、ITU、SMPTE和VESA规定。

本文将对不同的滤波器作一比较，以便根据给定的应用或制式确定最佳的设计。比较了Rauch和Sallen-Key两种类型滤波器的GBW与截止频率之比率，在设计中采用预失真与参量灵敏度技术来获得高精度。被考察的滤波器包括：

• ITU-601抗混叠滤波器
• 20MHz抗混叠与重建滤波器
• HDTV重建滤波器

滤波器及其特性不论是用于抗混叠还是重建，滤波器都必须具备低通特性，使视频的帧频能够通过。因此，设计者需要谨慎考虑AC耦合。低通滤波器可以根据其幅度特性或用于描述它的多项式来分类(Bessel、Butterworth、Chebyshev或Cauer)。图1所示为归一化为1-rad带宽后这些滤波器的特性。通常应该选取具有最佳选择性与最小极点数(降低成本)的滤波器，但是对相位线性度的额外要求限制了可选择的范围。


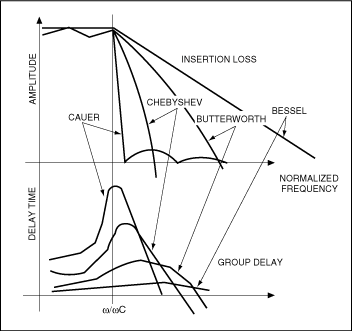
图1. 归一化为1-rad带宽后，各种滤波器的幅值和群延时与频率之间的关系 相位线性度与群延时滤波器的相位线性度决定了包络延时或群延时(GD)与频率的关系。平坦的群延时表明所有频率被延迟了相同的时间，在时域这有利于信号波形的保持。因此，群延时差异比绝对群延时更为重要。另有一项独立的参数称为通道间差异，用于衡量通道间的“时间符合度”，不应将其与群延时混淆。

对于视频来讲，多大程度的群延时差异是可以接受的，为什么？答案取决于具体的应用与视频制式。例如，ITU-470对复合视频信号群延时的规定非常宽松。然而，ITU-601则要严格许多，以便确保视频重放的稳定性，既针对于MPEG-2压缩，也是为了控制串行化之前的相位抖动。那么，为确保相位线性度，应该考虑什么样的滤波器特性呢？

图1中的群延时曲线在截止频率(ω/ωc = 1)处出现了一个峰。这是由截止频率附近陡峭的相位变化造成的。为了有一个大致的概念，以一个3极点、6MHzButterworth滤波器为例，在其带宽范围内群延时差异大约为20ns至25ns。增加极点数或滤波器的选择性会使该差异增加。其他一些用来减小群延时差异的更特殊的滤波器²包括Bessel、相位逼近、Thompson-Butterworth，以及LeGendre等。尽管如此，在视频中最常使用的仍然是Butterworth特性的滤波器。 分量视频的群延时问题所有视频制式与应用都对群延时差异敏感。敏感程度取决于信号的数量及其带宽。复合NTSC/PAL制式只有一路信号，群延时在ITU-470中有规定。该要求很容易满足。RGB与分量视频都包含多路信号。RGB信号各通道具有相同的带宽而分量视频则不同，因此对于RGB来讲群延时的匹配比较容易而分量视频则要困难一些。

因为Pb与Pr信号的带宽只有亮度(Y)信号的一半，所以它们的群延时是Y信号³的两倍。一种解决方法是加入延时级，使Y信号慢下来。另一种解决方法通过使Pb与Pr信号的采样率加倍，使信号带宽相等，即将4:2:2的采样率提高到4:4:44，这样就可将信号当作RGB来处理了。多出的Pb与Pr采样在抗混叠时被丢掉或在重建应用中被平均掉。

另一种分量视频制式，S-VHS，容易引起混淆。其Y通道与YPbPr制式相同，但色度信号(C)看起来更应该采用带通滤波，而不是低通滤波。对YPbPr信号而言，带通滤波会引起群延时与同步问题，所以不能采用。除非进行了模拟编码，Y和C信号可以采用相同的滤波器进行低通滤波。S-VHS在带宽方面带来的好处使它在延迟均衡方面的问题可以被谅解。S-VHS常见于视频重建应用中，此类应用主要关心的是Y与C之间正确的同步。 运放的选择选定了滤波器特性之后，下一步就是要用实际电路来实现它。最常用的单运放电路是同相配置的Sallen-Key滤波器与反相配置的Rauch滤波器。对工作在宽带视频应用中的运放而言，需要考虑的一个重要事项是最小增益-带宽(GBW)。视频信号是大幅度信号，典型为2VP-P，所以应考虑大信号GBW。不要将该参数与2VP-P 0.1dB GBW混淆，后者要小得多。

对滤波器电路来说，运放的GBW应该比滤波器的截止频率高多少？对于Rauch (反相)滤波器，相角参数为：

Arg[K(jω)]inv = -(ωc/GBWrad)(1 + Rf/Ri)

对于Sallen-Key (同相)滤波器：

Arg[K(jω)]noninv = π-(ωc/GBWrad)(1 + Rf/Ri)

其中，Rf与Ri为设定增益的电阻，单位为Ω，GBWrad为运放的增益带宽积，ωc为滤波器的截止频率，单位为弧度/秒。给定Rf与Ri5设定合适的增益，并解出(ωc/GBWrad)。单位增益Rauch电路中Rf/Ri = 1，Sallen-Key电路中Rf/Ri = 0。因此，对于相同的相位误差，Sallen-Key电路所需的GBW为Rauch电路的一半。随着所需增益的升高，它们在GBW方面的差距缩小，Sallen-Key滤波器的优势变小，但还有其他方面的问题需要考虑。 预失真、带宽、Q、以及参量灵敏度任何有限的GBWrad/ωc比率都会使滤波器的闭环极点发生偏移。这就是为什么实际滤波器的带宽ωc总是小于设计预期6。提升设计带宽可以补偿这个问题，这就是所谓的预失真技术。利用Sallen-Key与Rauch电路的计算公式(分别列于表1和表2)，我们可以计算出满足实际带宽要求的设计带宽。元件容差也必须考虑进来。

为了确定元件容差，引入一个灵敏度因数7：SXY，它是元件X的参数变化量与它所引起的参量Y变化量之比率。举例来讲，表1显示Sallen-Key电路中的Q对C1 与C2 的变化有比较大的灵敏度(对比Rauch电路)。这意味着Sallen-Key电路对寄生参数的容忍度比Rauch电路要低。关键在于，SXY使我们对这种效应有所预测，并在设计中采取相应的对策。接下来就可以考虑一些典型设计了。

表1. 元件灵敏度及BW与Q预失真公式(Sallen-Key类型，ωO = 1rad/s) SensiTIvity FuncTIon SXY Gain K = 3 - 1/Q
(R1 = R2 = C1 = C2 = 1) Gain K = 1
(R1 = R2 = 1) Gain K = 2
(R1 = C1 = 1) SXω (x = R1, R2, C1, C2) -1/2 -1/2 -1/2 SKQ 14 50 10 SR1Q 4.5 0 4.5 SR2Q -4.5 0 -4.5 SC1Q 9.5 1/2 5.5 SC2Q -9.5 -1/2 -5.5 SRaK -9/14 N/A -1/2 SRbK 9/14 N/A 1/2 ωc (actual) ωc (design)
[1 - 1/2(3 - 1/Q)2ωc / GBW] ωc (design)
[1 - ωcQ / GBW] — Q (actual) Q (design)
[1 + 1/2(3 - 1/Q)2ωc / GBW] Q (design)
[1 + ωcQ / GBW] —
表2. 元件灵敏度及BW与Q预失真公式(Rauch类型，ωO = 1rad/s) SensiTIvity FuncTIon SXY Gain K = 1
(R1 = R2 = R3 = 1) Gain K = 2
(R1 = 1, R3 = Ho, R2 = (Ho / 1 + Ho)) Gain K = 2
(C1 = 1, C2 = C1 / 100) SXω (x = R1, R2, C1, C2, SR1ω = 0) -1/2 -1/2 -1/2 SR1Q 1/3 1/3 1/3 SR2Q -1/6 0 0 SC1Q 1/2 1/2 1/2 SC2Q -1/2 -1/2 -1/2 SR3K 1 1 1 SR1K -1 -1 -1 SR3Q 1/6 0 0 ωc (actual) ωc (design)
[1 - 3ωcQ / 2GBW] — — Q (actual) Q (design)
[1 + 3ωcQ / 2GBW] — — 抗混叠滤波器的设计对于抗混叠滤波器，选择性由ITU-601规定的模板来确定，就像图2中所显示的。带宽规定为5.75MHz ±0.1dB，插损在6.75MHz处为12dB，8MHz处为40dB，0.1dB带宽范围内群延时差异为±3ns。这样的性能要求对于单纯的模拟滤波器来讲太困难了，但是通过四倍过采样可以将该要求调整为27MHz处12dB，32MHz处40dB。


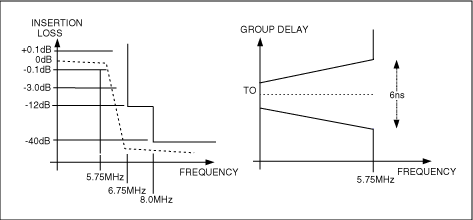
图2. 这个滤波器模板代表ITU-R BT.601-5标准所要求的抗混叠滤波

使用软件或归一化曲线8，我们会发现-3dB带宽为8.45MHz的5极点Butterworth滤波器就能满足选择性要求，但没考虑群延时。对于后者，需要一个延时级，对于此电路，需要重点关注的运放参数为0.1dB，2VP-P带宽9。将该数值应用于式1和2可获得精确的设计。图3a与3b给出了一个适合此类应用的原理图，并用曲线显示了它的增益和群延时特性，此设计基于四倍过采样系统。


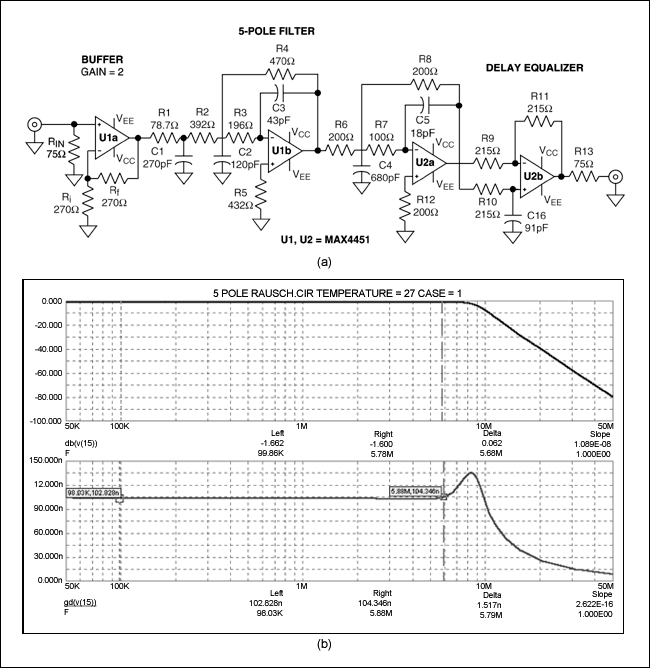
图3. 此原理图(a)与输出响应(b)表示的是针对ITU-601抗混叠的5极点5.75MHz Butterworth滤波器，采用的是Rauch电路与延时均衡器。

接下来要考虑的是PC视频。VESA没有为抗混叠或重建滤波器规定模板。XGA分辨率(1024 x 768，85Hz)具有94.5MHz的采样率，Nyquist 频率为47.25MHz。为在Nyquist频率处得到> 35dB的衰减量，采用Rauch类型的20MHz、4极点Butterworth滤波器(图4a和4b)。由于MAX4450/MAX4451卓越的瞬态响应与大信号带宽(2VP-P时175MHz)，因此仍然选择它。


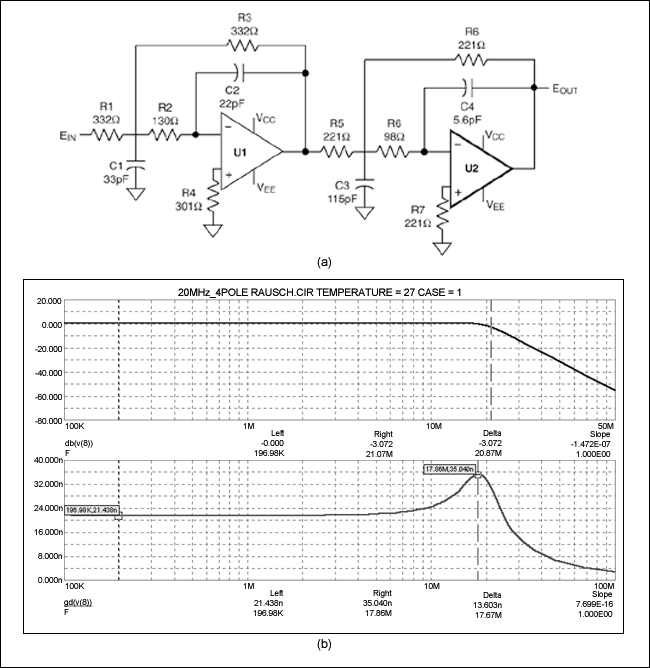
图4. 该原理图(a)与输出响应曲线(b)描述的是一个用于XGA图像抗混叠的4极点20MHz Butterworth滤波器，采用了Rauch电路。 重建滤波器DAC之后的重建滤波是没有被很好理解的应用之一。很多设计者认为引入重建滤波器是为了滤掉采样时钟，但这远不是事实。当信号被采样时，采样中包含了多个重复的信号映像，分别对准采样时钟的各次谐波。重建滤波器将滤掉除基带采样外的所有其他信号。如果抗混叠滤波器达到了其目的，那么DAC输出看上去就像图5中的映像A，接下来，它右边的所有采样都应被滤掉。因此，对于重建的要求类似于抗混叠，但是，由于每个采样只停留瞬间，DAC会将每个采样保持一个时钟周期，这样一来，就产生了我们所熟悉的逼近于某斜线的台阶状波形。


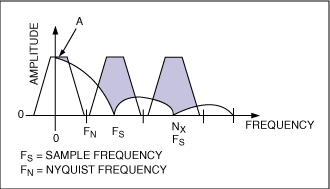
图5. 典型的DAC输出频谱与采样频率(FS)及Nyquist频率(FN)之间的关系

保持功能相当于一个数字滤波器，它的特性10类似于Butterworth或Bessel滤波器(图6)。注意到在半采样频率处响应被降低了4dB。重建滤波器的第二个目的是补偿这个损失，这就需要如图7a电路那样的幅度均衡器。该均衡器在一个延时电路的基础上构成，具有类似于Bessel滤波器的响应。它可按照DAC采样率(FS)来设计。图7b显示了采用和未用幅度均衡器时的DAC频率响应。与延时级类似，它可以被包含在任何重建滤波器中。


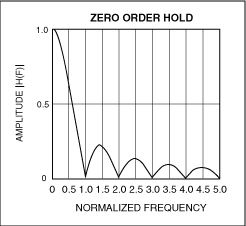
图6. DAC的“保持”功能产生了一个(sinx)/x响应，零点位于采样频率的整数倍处。


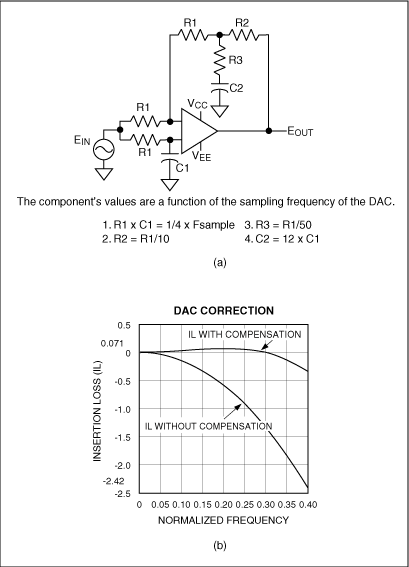
图7. 该图显示了DAC输出(b)带或不带(sinx)/x纠正(由幅度均衡器电路(a)提供)时的情况

保持响应也有一个对准采样时钟的极点，可以完全消除时钟。不过，大多数重建应用还是将时钟衰减作为其品质因数。现在了解了重建滤波器的功能，我们就可以着手设计了。

NTSC/PAL视频重建最普通的要求是在13.5MHz处衰减> 20dB，在27MHz处> 40dB，ωc取决于所采纳的视频标准。出于两方面的原因，我们选择了Sallen-Key结构的3极点Butterworth滤波器。首先，其增益(+2)适合驱动反向端接的电缆。其次，它的群延时差异可以调节，这样，不需要延时均衡器我们就可以通过调节群延时获得最优的性能(图8a至8d显示了NTSC和PAL设计，以及它们的增益和群延时特性)。这些应用通常包含了对于DAC的数字幅度修正，如有必要也很容易添加进来。


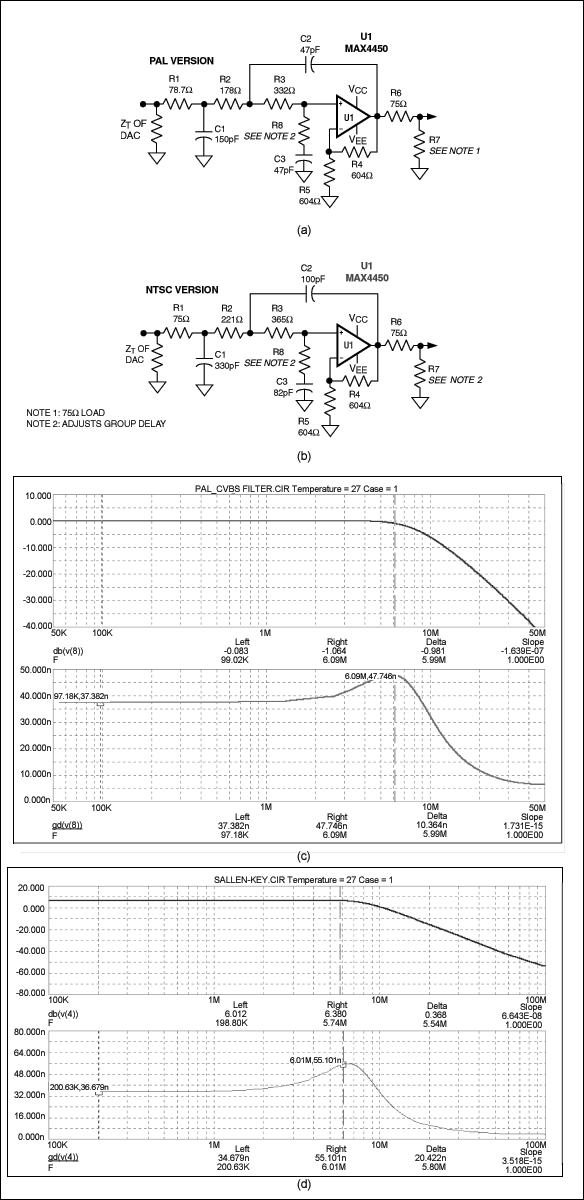
图8. 对带群延时调节的重建滤波器，PAL版本(a)的幅值与群延时响应曲线如(c)所示，NTSC版本(b)的幅值与群延时响应曲线如(d)所示。

还展示了一个用于XGA的电路，它是采用Sallen-Key结构的20MHz、3极点Butterworth滤波器，为实现幅值修正，其中还包括了图8中的电路(图9a和9b)。作为图4 抗混叠滤波器的补充，该滤波器具有+2的增益，用来驱动反向端接的75Ω同轴电缆。


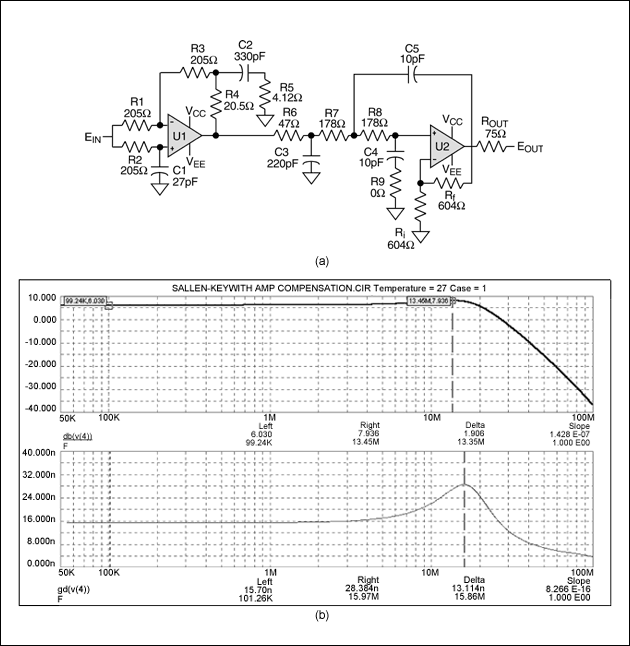
图9. 用于XGA重建的含(sinx)/x补偿的3极点20MHz Butterworth滤波器(a)，其输出响应曲线如(b)所示。

最后一个应用是用于HDTV的重建滤波器。根据SMPTE 274与296M规定的模板，它的中心频率ωc = 0.4 x FS = 29.7MHz。对于DAC的幅度纠正通常已经内含了，但群延时补偿必须外加。结果是一个30MHz、5极点Sallen-Key滤波器(图10)，74.25MHz时衰减> 40dB，还包括一个有+2倍增益的群延时级，以便驱动反向端接的75Ω同轴电缆。


图10. 用于HDTV的5极点30MHz重建滤波器，包括DAC幅值修正。 有源视频滤波器设计中的实际问题无论是手工设计的，还是软件辅助设计的，或是综合这两种方法得到的滤波器，实际的响应曲线可能并不完全符合预期。原因之一是计算出的响应与采用标准元件值得到的实际响应之间存有偏差。

选择标准(5%)容值的电容器而导出电阻值可以使误差降至最小。原因很现实—可以购得1%或2%容差的电容器，但容值精度仅为5%，而对电阻来说，1%容差和1%精度的电阻很容易得到。这样选择的元件可以提供最佳的一致性和最精确的幅度响应。

滤波器构成之后，可能出现不稳定与振荡的情况。如果出现这样的情况，将输入对地短接，看其是否继续振荡。如果振荡停止，说明阻抗太高，降低设计阻抗就可以消除振荡。但如果仍继续振荡，则请注意振荡频率是否接近滤波器的截止频率或在截止频率以下。如果是这样，振荡可能是由元件或寄生参数引起的。若振荡频率高于截止频率，那么可能是运放或电路板布局引起的。

好的布局就象是一件艺术作品，但它只是基于一些简单的原则。提供一个干净的电源电压和一个坚实的接地很重要，这意味着用低ESR的电容器滤波，有时是一个调节器。旁路电容连接而成的回路必须尽量小，否则寄生电感将与电容谐振。良好的接地平面对好的模拟设计很关键，但是随着带宽的增加，它可能带来寄生电容，使滤波器失调。为避免这样的问题，将受到影响的元件与走线下方的地平面去掉即可。

参考文献

1. 在截止频率处，滤波器响应下降-3dB。
2. Taylor和Williams，Electronic Filter Design Handbook，McGraw Hill，ISBN 0-07-070441-4。
3. 同前。
4. 4:2:2采样最初代表彩色副载波的过采样倍数。ITU-601将副载波频率改为3.375MHz。4:2:2表示分别在13.5MHz与6.75MHz下采样。
5. 在同相情况下，Rf/Ri = 0；在反相情况下Rf/Ri = 1。
6. E.J. Kennedy，Operational Amplifier Circuits: Theory and Applications。
7. 由H.W. Bode在Network Analysis and Feedback Amplifier Design (D. Van Nostrand, Princeton NJ, 1945)中定义。
8. Taylor和Williams, op. cit。
9. MAX4450/MAX4451数据资料。
10. 数学中的Sinc函数就是(sinx)/x。