同步时序逻辑电路的设计分析

在组合逻辑电路中，任一时刻的输出信号仅仅由该时刻的输入信号决定；而在时序电路中，任一时刻的输出信号不仅与当时的输入信号有关，而且与电路原来的状态有关。也就是说，时序电路中除具有逻辑运算功能的组合电路外，还必须有能够记忆电路状态的存储单元或延迟单元，也就是Latch & Flip-flop.

既然时序电路是有记忆功能地，那有几个概念必须是要清楚的：输入信号、输出信号、激励信号以及现态、次态及其转换关系。

时序逻辑电路的基本模型可以用下图表示：

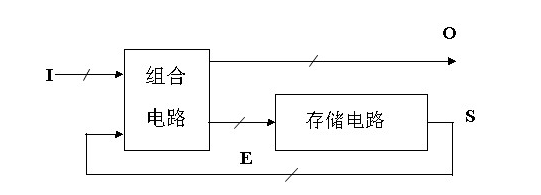
其中，I=（I1，I2，I3，···Ii）为时序电路的输入信号，O= （O1，O2，O3，···Oj）为时序电路的输出信号，E=（E1，E2，E3，···Ek）为驱动存储电路转换为下一个状态的激励信号，而S=（S1，S2，S3，···，Sm）为存储电路的的状态信号，亦称为状态变量也就是现态。可以看到状态变量S又反馈到组合电路的输入端，与输入信号I一起决定时序电路的输出信号O，并产生对存储电路的激励信号E，从而确定其下一个状态，即次态。这4组变量间可以列出三个向量函数形式的方程来表达：

O = f（I，S）;　　　　 输出方程

E = g（I，S）;　　　　　　激励方程

Sn+1 = h（E，Sn）;　　 状态方程

时序电路是状态依赖，故又称为状态机。我们只学习有限数量的存储单元构成的状态机，称为有限状态机（FSM:Finite State Machine）。有限状态机也分为两种：Mealy & Moore.

Mealy：

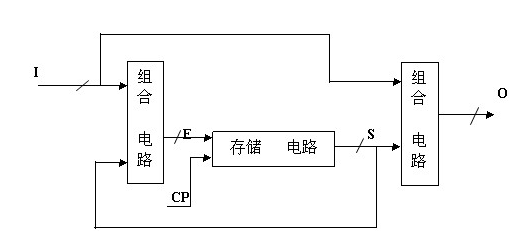
Moore：

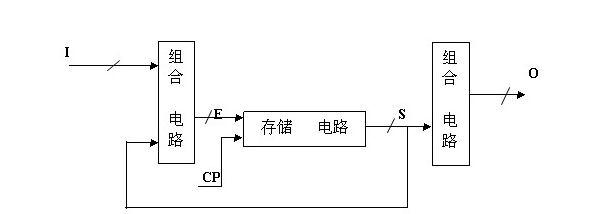
可以看出如果时序逻辑的输出不但取决于状态还取决于输入，称为Mealy状态机。而有些时序逻辑电路的输出只取决于当前状态，这样的电路就称作为Moore状态机。

时序电路又可以分为异步时序电路和同步时序电路两大类。简单的说若电路中触发器的时钟输入端没有接在统一的时钟脉冲上，或电路中没有时钟脉冲（如SR锁存器构成的时序电路），电路中各存储单元的状态更新不是同时发生的，则这种电路称为异步时序电路。根据电路是对脉冲边沿敏感还是对电平敏感，异步时序电路又分为脉冲异步时序电路（由触发器构成）和电平异步时序电路（由锁存器构成）两种。异步时序电路的状态转换取决于以任意时间间隔变化的输入信号序列，各存储单元的状态转换因存在时间差异而可能造成输出状态短时间不稳定，而且这种不稳定的状态有时是难以预知的，常常给电路设计和调试带来困难。与异步时序电路不同，同步时序电路中存储电路状态的转换是在同一脉冲边沿作用下同步进行的，也称作时钟同步状态机。同步时序电路的存储电路一般由触发器实现，所有触发器的时钟输入端都应接在同一个时钟脉冲源上，不会出现不稳定的状态。更重要的是，其电路的状态很容易用固定周期的时钟脉冲边沿清楚的分离为序列步进，很容易分析和设计。

组合电路的逻辑功能可以用一组输出方程来表示，也可用真值表和波形图来表达。相应地，时序电路可用方程组，状态表，状态图和时序图来表达。方程组就包含了输出方程组，激励方程组和状态方程组。一般的状态图表达的比较直观。

同步时序电路的分析：

（1） 根据给定的同步时序电路列出下列逻辑方程组：

a， 对应每个输出变量导出输出方程，组成输出方程组。

b， 对应每个触发器导出激励方程，组成激励方程组。

c， 将各触发器的激励方程代入相应触发器的特征方程中，得到各触发器的状态方程，从而组成状态方程组。

（2） 根据状态方程组和输出方程组，列出电路的状态表，画出状态图或时序图。

（3） 确定电路的逻辑功能，必要的话，可用文字详细描述。

同步时序逻辑电路的设计：

（1） 有给定的逻辑功能建立原始的状态图和原始的状态表，具体的做法是：

a，明确电路的输入条件和相应的输出要求，分别确定输入变量和输出变量的数目和名称。

b， 找出所有可能的状态和状态之间的转换关系。

c， 根据原始状态图建立原始的状态表。

（2） 状态简化：原始的状态图/表中可能隐含了多余的状态，去除它们，以减少触发器和门电路的数量。状态简化式建立在等价状态的基础之上：如果两个状态作为现态，其任何相同输入所产生的输出及建立的次态均完全相同，则这两个状态称为等价状态。

（3） 状态分配：对每个状态指定一个二进制码，也叫状态编码。这就涉及到编码方式的不同电路的性能也就不一样。

（4） 选择触发器类型。

（5） 确定激励方程组和输出方程组。

（6） 画出电路图，并检查自启动能力。

这些是基础没有这些是不行的，只有这些那是远远不够的，之所以照着书写这么多看似没用的东西一是帮我建立一些基本概念，二是让我沉下心来。接下来就是要练习，不断的练习，代码是堆出来的，当然更要进一步的学习、总结。