
在很多情况下,DTMF译码器输出的数据仍需送入单片机进行相应的运算及处理,进而控制其它各种设备的动作。因此,如果能找到一种基于单片机的DTMF信号的译码算法,再辅之以简单的整形电路就可以,既可省去成套译码电路,又能达到简化电路降低成本的目的
本文所要介绍的,就是这种构想的初衷,结果通过计算机仿真计算数据论证认为完全能够达到设计要求。
1、DTMF信号频率组成及整形前DTMF信号的幅值密度
在DTMF信号中,16个指令键均由两个单音频率信号组合(见表1)。单音频率有两组,高频组为(1209Hz、1336Hz、1447Hz、1633Hz),低频组为(697Hz、770Hz、852Hz、941Hz),每个指令键,对应的都是一个高频组的频率和一个低频组的频率的组合。以“*”号指令键为例:其DTMF信号是由941Hz的低频组信号和1209Hz的高频组信号组成。图1为其频谱图。
表1 DTMF信号频率组成表
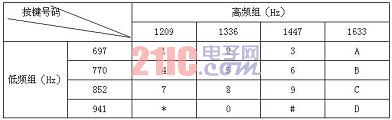

从图1中可以看出,“*”号指令键的DTMF信号在941Hz和1209Hz处有谱线。在理想条件下,可计算出频谱密度函数X(f)在f=941Hz和1209Hz时的模值为|X(941)|,|X(1209)|,即它们模值均不为零。也就是说,要是同时存在频谱密度函数模值为|X(941)|,|X(1209)|,并且它们模值均不为零时,其表征的键号为“*”。以此类推(见表1),可分别计算出低频组信号|X(697)|、|X(770)|、|X(852)|、|X(941)|和高频组信号|X(1209)|、|X(1336)|、|X(1447)|、|X(1633)|的模值。如果高、低频组中均各自有一个X(f)的模值不为零,则再通过f在表1查找出其表征的指令键。
在用单片机进行X(f)运算即离散傅立叶变换(DFT)时,只能对有限长的DTMF信号进行分析与处理,即对有限时间Tp=NT内的N个数据进行离散傅立叶变换(N为采样点数,T为采样时间间隔)。
根据DFT定义式:

同样以“*” 指令键信号为例,在高频率组f=1209 Hz,采样点数N=256,采样时间间隔T=55×10-6 S时,由式K=f×N×T,可得K=17,即|X(17)|为DTMF信号在频率为1209 Hz处的幅值密度其值为121.5。在低频率组f=941 Hz,采样点数N=256,采样时间间隔T=54×10-6 S时,由式K=f×N×T,可得K=13,即|X(13)|为DTMF信号在频率为941 Hz处的幅值密度其值为123.6。同理,可计算出其它15个指令键的幅值密度,见表2(表2为对16个指令键的DTMF信号采用计算机仿真计算后的幅值密度)。
表2 整形前DTMF信号的幅值密度表
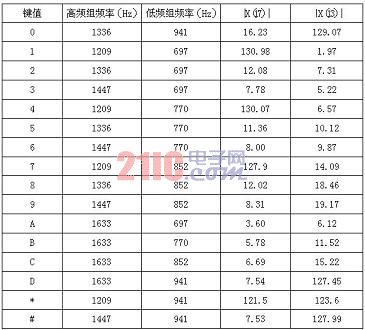
从表2看出:由于时域无限长DTMF信号被截断所引起的泄漏效应,如“2”、“3”号键对应的DTMF信号虽然不含有频率为1209 Hz和941 Hz的信号成份,可是|X(17)|、|X(13)|不为零,理想时应为零,也就是说存在一定的幅值密度误差。但对于含有f=1209 Hz高频组信号的DTMF信号(如“1”、“4”、“7”、“*”键),其|X(17)|值远大于不含f=1209 Hz高频组信号的DTMF信号的|X(17)|值。同样,对于含有f=941 Hz低频组信号的DTMF信号的|X(13)|值远大于不含f=941Hz低频组信号的DTMF信号的|X(13)|值,这样就为实际DTMF信号译码识别提供了必要的条件。因在实际DTMF信号译码应用时,任一键号所对应的DTMF信号的译码过程为:
(1)分别采样DTMF信号计算出谱线为697Hz、770Hz、852Hz、941Hz的幅值密度|X(k)|。
(2)从中排序找到低频组频率fL对应幅值密度|X(k)|最大的值。
(3)同法计算,谱线为1209Hz、1336Hz、1467Hz、1633Hz的幅值密度|X(k)|。
(4)从中排序找到高频组频率fH对应幅值密度|X(k)|最大的值。
(5)根据fL、fH查表1,即可得到其所表征的键号。
2、整形后DTMF信号的幅值密度及其实验数据误差分析
为了把DTMF信号送入单片机进行DTMF信号译码,还必须要对DTMF信号进行整形,见图2所示。DTMF信号经比较限幅,整形为方波后。从DFT变换定义式看出:式中x(nT)的值只能为0或者1,因此计算|X(k)|的运算量大大降低,表3即为通过整形后DTMF信号采用计算机仿真计算出的幅值密度。
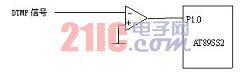
图2 DTMF信号比较限幅示意图
表3 整形后DTMF信号的幅值密度表
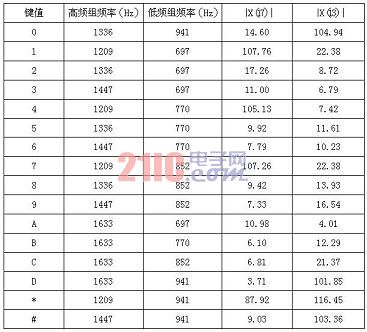
对比表3和表2可以发现,整形为方波后的DTFM信号泄漏谱线的幅值密度有所增大,而有效谱线的幅值密度也相应变小。例如7号指令键产生的泄漏谱线的幅值密度其值从14.09增大到22.38,而有效幅值密度其值从127.9减小到107.26。造成此类问题的主要原因是:
(1)由于N,T只能选择整数,1/f不可能被N×T所整除,所以这必然会带来栅栏效应,此时计算所得的有效谱线的幅值密度必然 小 于 实 际 值 。同 时 ,由于采样时间Tp=NT有限长而引起的泄漏效应,也必然会导致泄漏谱线的幅值密度增大。
(2)DTMF信号经整形为方波后会产生了十分丰富的谐波干扰,这些干扰信号的频率如果接近泄漏谱线的频率,也会使泄漏谱线的幅值密度增大。
因此在译码过程中,如果有效谱线的幅值密度值变小,而泄漏谱线的幅值密度增大,当泄漏谱线的幅值密度大于有效谱线的幅值密度时,就会引起错译和漏译现象。所以在N×T值选择过小,或者与待测周期的整数倍相差过大,再加上整形为方波后谐波干扰,将有可能引起错译和漏译。
但是从表3中可见泄漏谱线的幅值密度最大值为22.38,而有效谱线的幅值密度最小值为87.92两者相差近4倍,还存在较大的冗余量。例如:对于含有f=1209 Hz高频组信号的DTMF信号(如“1”、“4”、“7”、“*”键),其|X(17)|值仍远大于不含f=1209 Hz高频组信号的DTMF信号的|X(17)|值。同样,对于含有f=941 Hz低频组信号的DTMF信号的|X(13)|值也远大于不含f=941Hz低频组信号的DTMF信号的|X(13)|值,二者仍可在排序中明显区分出来,所以对DTMF信号整形后产生的一定幅值密度误差增大,完全可以忽略不计,只要译码应用程序设计得当,合理选取N、T值,不会出现错译和漏译现象。
在DTMF信号比较准确或干扰较小的场合,甚至还可以通过减少N,T的值来提高运算速度,减少译码时间。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)