
1 引言
追尾碰撞是目前我国高速公路各类事故中较多的一类事故,占事故总数的33%左右。根据对沈大、合宁、广深、西临等高速公路交通事故的统计分析,交通事故类型如表1所示。
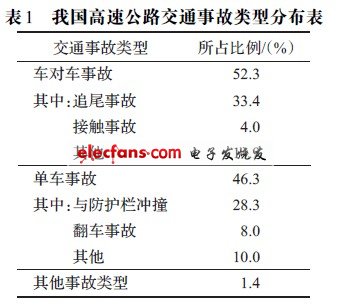
有关研究表明,若驾驶员能够提早1 秒意识到有事故危险并采取相应的措施,则90%的追尾事故和60%的正面碰撞事故都可以避免。美、英、德、日的不少汽车公司(如德国的奔驰、日本的三菱、马自达、日产、本田及富土重工等公司)都开展了高速公路车载毫米波雷达防追尾碰撞预警系统的研究。
我国主要有清华大学、浙江大学、上海交通大学、吉林大学等高校和部分研究所在进行车辆主动防撞报警、辅助驾驶系统等相关技术研究。例如上海交通大学卓斌教授等研究开发了“人—车—路综合环境下主动安全性模拟系统”,实现了行车环境数据采集、通讯和驾驶软件仿真的编制。在现行的高速公路交通管理中,为保证行车安全,常依据公路工程技术标准中的行车视距要求,规定一定行驶速度下的车辆必须保持相应的间距。那么如何准确跟踪车辆之间的距离信息,就成了汽车毫米波雷达防追尾预警系统的关键。
把交互多模型(IMM)机动目标跟踪算法运用到汽车毫米波雷达防追尾预警系统当中,当毫米波雷达存在一定测量误差和噪声时,目标跟踪算法能使毫米波雷达能够准确地探知前方车辆的运动状态,如车间距离、行驶速度等,从而提高驾驶员在高速公路上行驶安全性。
2 汽车防追尾预警系统工作原理
高速公路汽车防追尾预警系统由信息采集单元、信息处理单元和信息输出装置3 部分组成。信息采集单元通常由毫米波雷达、自车速度传感器、转向角传感器、制动传感器、加速踏板传感器和路面情况选择开关等组成;信息处理单元主要为中央处理器;信息输出装置包括液晶显示屏、报警蜂鸣器、报警指示灯等,图1 是车载雷达防追尾预警系统组成方框图。
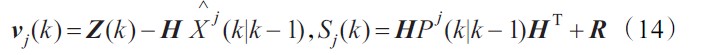
信息采集单元不断地采集相关信息,利用车载毫米波雷达获得前方目标车辆的运动信息,如车间距离、相对速度;利用自车传感系统获得自车运行状态信息,如自车速度、有无转向、有无制动等,并将此信息传送至信息处理单元。信息处理单元根据自车速度、相对速度以及所建立的安全距离计算模型,计算出当前应保持的安全距离并与实测车间距离相比较。若实测车间距离大于提醒报警距离,则进入下一工作循环;若实测车间距离小于提醒报警距离,则进行一次报警,提醒驾驶员松油门并做好刹车准备;当实测车间距离小于危险报警距离,则进行二次报警,促使驾驶员立即制动,以避免追尾事故的发生。液晶显示屏用于显示两车间实际距离及相对速度,报警蜂鸣器和报警指示灯用于提供声音报警和指示灯报警,及时的报警可以有效地提醒驾驶员,促使其采取合适的应对措施。
汽车在道路上行驶时,经常要进行加速、减速和转弯,其运动状态是不断改变的。行驶中的汽车所处的道路环境是相当复杂的,而安装车载毫米波雷达的汽车本身也是不时地处于机动状态之中,因此车载雷达所探测的目标也是在不停的变化当中,导致所测两汽车之间的距离数据存在一定测量误差和噪声,就会使汽车防追尾预警系统产生虚警或漏警。过高虚警率的雷达不但不能减轻驾驶者的工作负担,反而会造成驾驶者精神高度紧张,起到相反的效果。因此,采用合适的机动目标跟踪算法,准确地跟踪自车前面的车辆目标的状态、及时估计行车的危险程度是车载雷达测距系统的一项主要任务。
3 交互多模型机动车辆跟踪算法
交互多模算法是Blom和Bar-Shalom在多模型基础上提出的,是在广义伪贝叶斯算法基础上,以卡尔曼滤波为出发点,提出的一种具有马尔可夫切换系数的交互式多模型算法,其中多种模型并行工作,目标状态估计是多个滤波器交互作用的结果。该算法不需要机动检测,同时达到了全面自适应能力。IMM算法的基本思想是在每一时刻,假设某个模型在现在时刻有效的条件下,通过混合前一时刻所有滤波器的状态估计值来获得与这个特定模型匹配的滤波器的初始条件;然后对每个模型并行实现正规滤波(预测与修正)步骤;最后,以模型匹配似然函数为基础更新模型概率,并组合所有滤波器修正后的状态估计值(加权和)以得到状态估计。一个模型有效的概率在状态估值和协方差的加权综合计算中有重要作用。IMM的设计参数为:不同匹配和结构的设置模型;不同模型的处理噪声密度(一般来讲,非机动模型具有低水平测量噪声,机动模型具有较高水平的噪声);模型之间的切换结构和转移概率。与其他的机动目标的跟踪算法相比,比如辛格(Singer)算法、输入估计(IE)算法、变维滤波(VD)算法等,交互多模(IMM)算法的优点是它不需要机动检测器监视机动[10],从而不会产生因模型在机动与非机动之间切换而带来的误差。其算法原理如下:
假定有r 个模型:
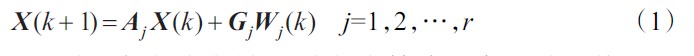
其中X(k)为目标状态向量,Aj为状态转移矩阵,Gj为系统噪声作用矩阵,Wj(k)是均值为零,协方差矩阵为Qj的白噪声序列。
可用一个马尔可夫链来控制这些模型之间的转换,马尔可夫链的转移概率矩阵为:
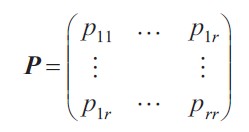
测量模型为:

其中Z(k)为量测向量,H为观测矩阵,V(k)为量测噪声,已知其方差为R(k)。W(k)和V(k)是零均值且相互独立。
IMM算法可归纳如下4 个步骤。
步骤1 输入交互:
根据两模型(k-l)时刻的滤波值和模型概率,计算交互混合后的滤波初始值,包括模型1 的滤波初始值:滤波估计值X 01
(k - 1)和估计协方差μ1(k - 1);模型2 的滤波初始值:滤波估计值X 02
(k - 1)和估计误差协方差P02
(k - 1)。设系统在(k-1)时刻模型1 概率为μ1(k - 1),滤波值X1
(k - 1),估计误差协方差为P2(k - 1)。模型2 的概率为μ2(k - 1),滤波值为X 2
(k - 1),系统估计误差协方差为P2(k - 1)。则进一步推广到r 个模型,交互后r模型的滤波初始值为:


步骤2 模型条件滤波:
对应于模型Mj(k),以X 0j
(k - 1|k - 1),P0j(k - 1|k - 1)及Z(k)作为输入进行卡尔曼滤波。
卡尔曼预测方程:
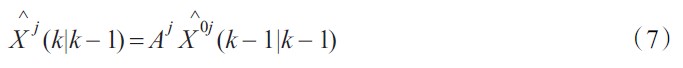
预测误差协方差阵:
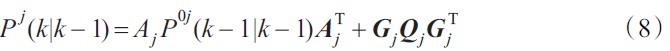
卡尔曼增益:
![]()
滤波方程为:
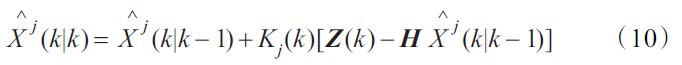
波误差方差阵:

步骤3 模型概率更新:

i = 1rΛj(k)cj_,而Λj(k)为观测Z(k)的似然函数:

其中:
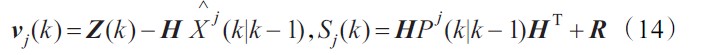
步骤4 输出交互:


图2 为IMM算法结构原理图
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)