
当RF工程师首次计算哪怕是最好的低噪声高速ADC的噪声系数时,结果也可能相对高于典型RF增益模块、低噪声放大器等器件的噪声系数。为了正确解读结果,需要了解ADC在信号链中的位置。因此,当处理ADC的噪声系数时,务必小心谨慎。
ADC噪声系数定义
图1显示了用于定义ADC噪声系数的基本模型。噪声因数F指的是ADC的总有效输入噪声功率与源电阻单独引起的噪声功率之比。由于阻抗匹配,因此可以用电压噪声的平方来代替噪声功率。噪声系数NF是用dB表示的噪声因数,NF = 10log10F。

图1:ADC的噪声系数:小心为妙!
该模型假设ADC的输入来自一个电阻为R的信号源,输入带宽以fs/2为限,输入端有一个噪声带宽为fs/2的滤波器。还可以进一步限制输入信号的带宽,产生过采样和处理增益,稍后将讨论这种情况。该模型还假设ADC的输入阻抗等于源电阻。许多ADC具有高输入阻抗,因此该端接电阻可能位于ADC外部,或者与内部电阻并联使用,产生值为R的等效端接电阻。
ADC噪声系数推导过程
满量程输入功率是指峰峰值幅度恰好填满ADC输入范围的正弦波的功率。下式给出的满量程输入正弦波具有2VO的峰峰值幅度,对应于ADC的峰峰值输入范围:
![]()
该正弦波的满量程功率为:
ADC噪声系数推导过程
满量程输入功率是指峰峰值幅度恰好填满ADC输入范围的正弦波的功率。下式给出的满量程输入正弦波具有2VO的峰峰值幅度,对应于ADC的峰峰值输入范围:
![]()
该正弦波的满量程功率为:

通常将此功率表示为dBm(以1 mW为基准):

对 滤波器的噪声带宽B需要加以进一步的讨论。非理想砖墙滤波器的噪声带宽指的是让相同的噪声功率通过时,理想砖墙滤波器所需的带宽。因此,一个滤波器的噪声 带宽始终大于其3 dB带宽,二者之比取决于滤波器截止区的锐度。图2显示了最多5极点的巴特沃兹滤波器的噪声带宽与3 dB带宽的关系。注意:对于2极点,噪声带宽与3 dB带宽相差11%;超过2极点后,二者基本相等。

图2:巴特沃兹滤波器的噪声带宽与3dB带宽的关系
NF计算的第一步是根据ADC的SNR计算其有效输入噪声。ADC数据手册给出了不同输入频率下的SNR,确保使用与目标IF输入频率相对应的值。此外还应确 保SNR数值中不包括基波信号的谐波,有些ADC数据手册可能将SINAD与SNR混为一谈。知道SNR后,就可以从下式开始计算等效输入均方根电压噪 声:
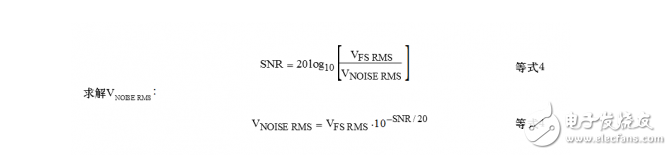
这是在整个奈奎斯特带宽(DC至fs/2)测得的总有效输入均方根噪声电压,注意该噪声包括源电阻的噪声。下一步是实际计算噪声系数。在图3中,注意源电阻引起的输入电压噪声量等于源电阻√(4kTBR)的电压噪声除以2,即√(kTBR),这是因为ADC输入端接电阻形成了一个2:1衰减器。
噪声因数F的表达式可以写为:

将F转化为dB并简化便可得到噪声系数:
![]()
其中,SNR的单位为dB,B的单位为Hz,T = 300 K,k = 1.38 × 10–23 J/K。

图3:根据SNR、采样速率和输入功率求得的ADC噪声系数
过采样和数字滤波会产生处理增益,从而降低噪声系数,这已在上文中说明。对于过采 样,信号带宽B低于f s /2。图4给出了校正因数,因而噪声系数的计算公式变为:

图4:过采样和处理增益对ADC噪声系数的影响
16位、80/100 MSPS ADC AD9446的计算示例

图 5显示了16位、80/105 MSPS ADC AD9446的NF计算示例。一个52.3 Ω电阻与AD9446的1 kΩ输入阻抗并联,使得净输入阻抗等于50 Ω。ADC在奈奎斯特条件下工作,82 dB的SNR是利用上式8进行计算的基础,得到噪声系数为30.1 dB。
图5:16位80/100 MSPS ADC AD9446 在奈奎斯特条件下工作的噪声系数计算示例
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)