基于PCA算法的人脸识别研究与实现

　　PCA算法主成分分析法

　　主成分分析（Principal Component Analysis，简称PCA）方法是目前应用很广泛的一种代数特征提取方法，可以说是常用的一种基于变量协方差矩阵对样本中的信息进行处理、压缩和抽提的有效方法，主要通过K-L（Karhunen-Loeve）变换展开式从人脸数据库中提取人脸的主要特征［i］，构成特征脸空间，在识别时将待测试的人脸图像投影到特征脸空间，得到一组投影系数，与数据库中各个人脸图像进行比对识别。

　　这种方法保留了原向量在与其协方差矩阵最大特征值相对应的特征向量方向上的投影，即主分量（Principal Components），因此被称为主成分分析。由于PCA方法在进行降维处理和人脸特征提取方面的有效性，在人脸识别领域得到了广泛的应用。它的核心思想是：利用较少数据的特征对样本进行描述以达到降低特征空间维数的目的，根据样本点在多维空间的位置分布，以样本点在空间中变化最大方向，即方差最大方向，作为差别矢量来实现数据的特征提取。利用K-L变换抽取人脸的主要成分，利用特征脸法进行人脸识别的过程由训练阶段和识别阶段两个阶段组成。

　　基于PCA算法的人脸识别研究

　　1 人脸识别的发展及现状

　　人脸识别的研究已经有很长的历史，在19世纪，法国人Galton就曾对此问题进行了研究，他用一组数字代表不同的人脸侧面特征来实现对人脸侧面图像的识别。国内外对于人脸识别的研究发展，分别经历了三个阶段：传统的人机交互式阶段、机器自动识别初级阶段、机器自动识别高级阶段。

　　1．1 传统的人机交互式阶段

　　第一阶段是以BerTIlion为代表，主要研究人脸识别所需要的面部特征，该阶段的识别依赖于人的 *** 作。这些人脸识别方法都需要利用 *** 作员的某些先验知识，仍然摆脱不了人的干预。

　　1．2 自动识别初级阶段

　　第二阶段主要是采用机器自动识别的手段进行识别，20世纪90年代以来，随着高速度高性能计算机的出现，人脸识别方法有了重大突破，进入了真正的机器自动识别阶段，人脸识别研究也得到了前所未有的重视。

　　1．3 机器自动识别高级阶段

　　第三阶段是真正利用机器进行对人脸的自动识别，随着计算机的大型化、高速化和人脸识别的方法的发展，提出了许多人脸自动识别的系统。

　　2 PCA算法的原理

　　PCA（主成分分析）算法是人脸识别中比较新的一种算法，该算法的优点是识别率高，识别速度快。

　　2．1 PCA算法介绍

　　2．1．1 PCA原理

　　令x为表示环境的m维随机向量。假设x均值为零，即：

　　E［x］=O．

　　令w表示为m维单位向量，x在其上投影。这个投影被定义为向量x和w的内积，表示为：

　　

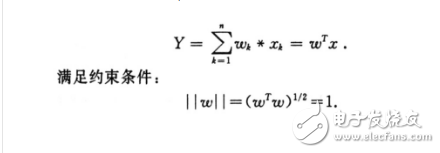
　　而主成分分析的目的就是寻找一个权值向量w使得表达式E［y2］的值最大化：

　　

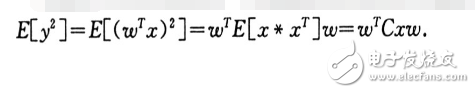
　　根据线性代数的理论，可以知道满足式子值最大化的训应该满足下式：

　　

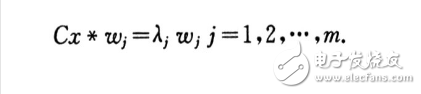
　　即使得上述式子最大化的w是矩阵Cx的最大特征值所对应的特征向量。

　　2．1．2 主成分的求解步骤

　　在PCA中主要的是要求出使得方差最大的转化方向，其具体的求解步骤如下：

　　（1）构建关联矩阵：Cx=E［x*xT］，Cx∈Pn*n.

　　在实际应用中，由于原始数据的数学期望不容易求解，我们可以利用下式来近似构造关联矩阵：

　　

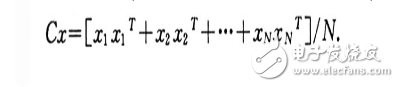
　　（其中x1，x2，…，xN，是各个原始灰度图像所有象素点对应的向量，N是原始图像的个数）

　　（2）先计算出Cx的各个特征值

　　（3）把特征值按大小排序

　　

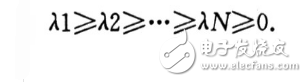
　　（4）计算出前m个特征值对应正交的特征向量构成w。

　　（5）将原始数据在特征向量w上进行投影，即可获得原始图像的主特征数据。

　　2．1．3 主成分的求解方法

　　通过上面的分析我们可以知道，对于主成分分析的问题最后转化为求解协方差矩阵的特征值和特征向量的问题，主成分的正交化分解的算法或求XXT特征值问题的算法常用的有雅可比方法和NIPALS方法。

　　2．2 Eigenface算法

　　在利用PCA进行特征提取的算法中，特征脸方法（Eigenface）是其中的一个经典算法。特征脸方法是从主成分分析导出的一种人脸识别和描述技术。特征脸方法就是将包含人脸的图像区域看作是一种随机向量，因此可以采用K-L变换获得其正交K-L基底。对应其中较大特征值的基底具有与人脸相似的形状，因此又称为特征脸。利用这些基底的线性组合可以描述、表达和逼近人脸图像，因此可以进行人脸识别与合成。识别过程就是将人脸图像映射到由特征脸构成的子空间上，比较其与己知人脸在特征空间中的位置，具体步骤如下：

　　（1）初始化，获得人脸图像的训练集并计算特征脸，定义为人脸空间，存储在模板库中，以便系统进行识别；

　　（2）输入新的人脸图像，将其映射到特征脸空间，得到一组关于该人脸的特征数据；

　　（3）通过检查图像与人脸空间的距离判断它是否是人脸；

　　（4）若为人脸，根据权值模式判断它是否为数据库中的某个人，并做出具体的 *** 作。

　　2．2．1 计算特征脸

　　设人脸图像I（x，y）为二维N*N灰度图像，用N维向量R表示。人脸图像训练集为{Ri|i=1，…，M}，其中M为训练集中图像总数，这M幅图像的平均向量为：

　　

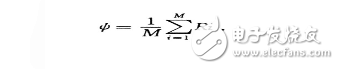
　　每个人脸Ri与平均人脸ψ的差值向量是：

　　

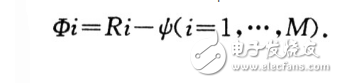
　　训练图像的协方差矩阵可表示为：

　　C=AAT.

　　其中，A=［φ1，…φM］。

　　特征脸有协方差矩阵C的正交特征向量组成。对于N*N人脸图像，协方差矩阵C的大小为N2*N2，对它求解特征值和特征向量是很困难的。一种取而代之的方法是令L=ATA．

　　即协方差矩阵的转置阵，则可以知道此矩阵是M*M（M是训练人脸的数量）的一个较小的矩阵。首先计算M*M矩阵L的特征向量vi（l=l，…，M），则矩阵C的特征向量ui（l=1，…，M）由差值图像φi（i=1，…，M）与vi（l=l，…，M）线性组合得到：U=［u1，…，uM］=［［ψ1，…，ψM］T］［v1．…，vM］。实际上，m（m《M）个特征值足够用于人脸识别。因此，仅取L的前m个最大特征值的特征向量计算特征脸。

　　3 PCA算法在人脸识别中的应用

　　基于特征脸的人脸识别过程由训练阶段和识别阶段两个阶段组成。在训练阶段，每个已知人脸Ri映射到由特征脸构成的子空间上，得到m维向量

　　

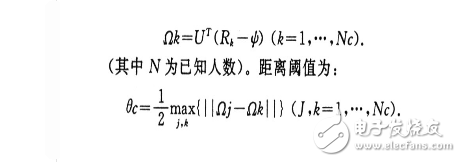
　　在识别阶段，首先把待识别的图像R映射到特征脸空间。得到向量：

　　

　　为了区分人脸和非人脸，还需计算原始图像R与其由特征空间重建的图像Rf之间的距离ε：

　　

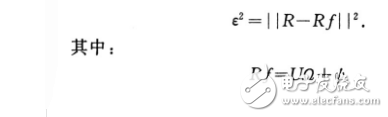
　　采用最小距离法对人脸进行分类，分类规则如下：

　　（1）若ε≥θc，则输入图像不是人脸图像；

　

　　4 实验结果

　　实验在两个图库上测试，首先是一个ORL人脸库，该库包含40个不同人物，每人有lO张图片，共400幅。用训练样本进行测试，识别率为95％。一个是自建人脸库，该库包含20个不同人物，每人有5张不同表情和姿态下的图片，总共100幅。随着训练样本的增加，识别率会有所提升，但是并不是越多越好，当超过一定的训练样本数目时，识别率反而有所下降。

　　5 人脸识别未来的发展

　　人脸识别是一个跨学科富挑战性的前沿课题，人脸图像中姿态、光照、表情、饰物、背景、时间跨度等因素的变化对人脸识别算法的鲁棒性都有着负面的影响，单一的PCA方法识别率不高，今后的发展方向可以与其他方法（如：支持向量机、小波变化等）相结合来弥补单一方法的不足，让身份识别更准确。