基于VerilogHDL语言的FIR数字滤波器设计与实现

　　引言

　　数字滤波器是语音与图像处理、模式识别、雷达信号处理、频谱分析等应用中的一种基本的处理部件， 它能满足波器对幅度和相位特性的严格要求， 避免模拟滤波器所无法克服的电压漂移、温度漂移和噪声等问题。有限冲激响应（FIR）滤波器能在设计任意幅频特性的同时保证严格的线性相位特性。

　　1 FIR 数字滤波器

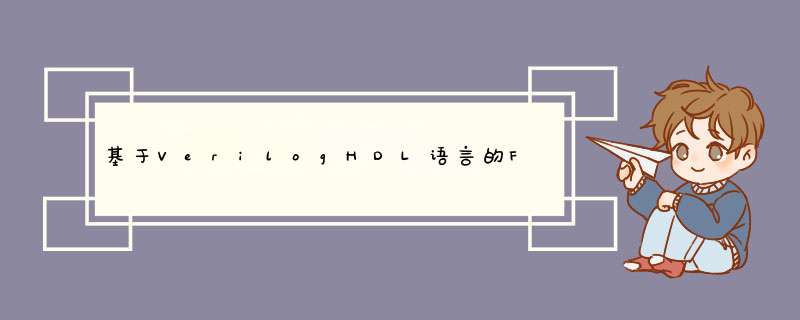
　　FIR 滤波器用当前和过去输入样值的加权和来形成它的输出， 如下所示的前馈差分方程所描述的。

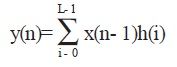
　　FIR 滤波器又称为移动均值滤波器， 因为任何时间点的输出均依赖于包含有最新的M个输入样值的一个窗。由于它的响应只依赖于有限个输入， FIR 滤波器对一个离散事件冲激有一个有限长非零响应， 即一个M阶FIR 滤波器对一个冲激的响应

　　在M个时钟周期之后为零。

　　FIR滤波器可用图1 所示的z 域块图来描述。

　　其中每个标有z- 1 的方框都代表了有一个时钟周期延时的寄存器单元。这个图中标出了数据通道和必须由滤波器完成的 *** 作。滤波器的每一级都保存了一个已延时的输入样值， 各级的输入连接和输出连接被称为抽头， 并且系数集合{hk}称为滤波器的抽头系数。一个M阶的滤波器有M+1 个抽头。通过移位寄存器用每个时钟边沿n（ 时间下标） 处的数据流采样值乘以抽头， 并且求和得到输出yFIR［n］。滤波器的加法和乘法必须足够快， 在下一个时钟来到之前形成y［n］。并且在每一级中都必须测量它们的大小以适应他们数据通道的宽度。在要求精度的实际应用中， LatTIce 结构可以减少有限字长的影响， 但增加了计算成本。一般的目标是尽可能快地滤波， 以达到高采样率。通过组合逻辑的最长信号通路包括M级加法和一级乘法运算。FIR 结构指定机器的每一个算术单元有限字长， 并且管理运算过程中数据流。