放大电路分析：三极管的微变等效电路

三极管的微变等效电路

将非线性器件线性化

在小信号变化量的条件下，用线性电路来描述三极管非线性特性，称为微变等效电路。

1 三极管的输入回路等效成一个动态电阻re

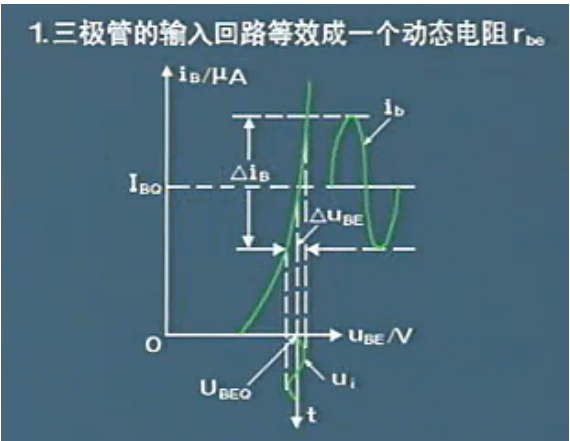
根据输入特性曲线找到Q点然后根据Q点做出对应的IBQ和UBEQ

以UBEQ为基本点加上一个正弦信号ui此时就会看到一个正弦的ib产生他们都是一个完美的正弦波形，

怎么才能让ib和ui波形一样变化呢，这个信号应该是足够小。我们怎么才能找到这个足够小的信号呢

以Q点为例，假如我们以Q点为切点做一条切线，这个切线能够和原来的输入特性曲线重合的假如你所取的信号是切线和输入特性曲线重合的那段变化量，那么我们就认为这个曲线变化是比较小的。

在这一段里面三极管表现出电阻的特性，他表示的是在这段切线和输入曲线重复的这一段中端电压和电流是一种线性关系。

这个电阻特性的物理意义是在这条切线和输入特性曲线对应的电压的变化量比上对应的电流的变化量，最后得到电阻。如下图

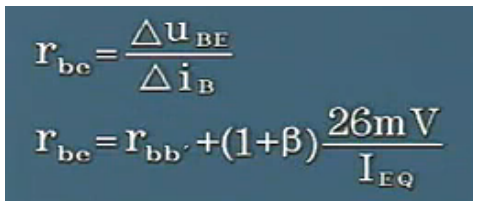
公式变量解释如下

其中rbb‘表示基区体电阻可以重手册中查到

IEQ表示在静态的时候发射结所流过的电流，这个电流和基电级流过的电流基本上相等。Q点越高IEQ越大，发射结的电阻越小。则整个三极管的输入回路等效电阻rbe也就越小，rbe是一个和Q点紧密相关的物理量。

三极管的输出回路等效为一个电流控制的电流源

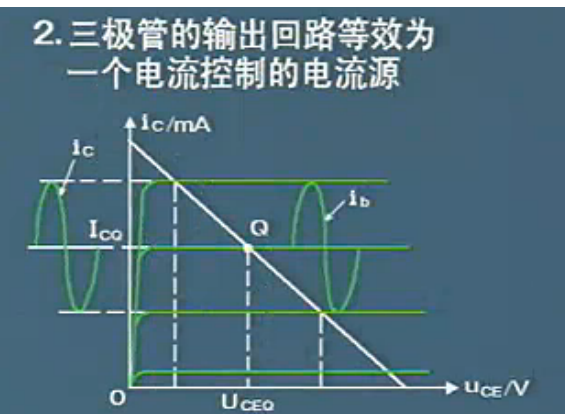
由图可以看出

当给一个ib的时候就会产生一个ic如果ib和ic都是完美曲线的时候可以得到ib和ic成beta（呗塔）倍的关系

ic完全按照beta（呗塔）倍ib关系线性变化

此时三极管工作在放大状态，也就是IBQ 都是平行于横轴，IBQ 都是等距离的则此时ic只受ib的控制和UCE无关

在输出特性曲线可以看出 当UCE变化的时候，在平行区里面UCE变大iC是不会改变的所以得到如下

上图中ic表示瞬时值 Ic表示有效值

由上图可以看出ic是指受ib控制的这里可以得到三极管的微变等效电路

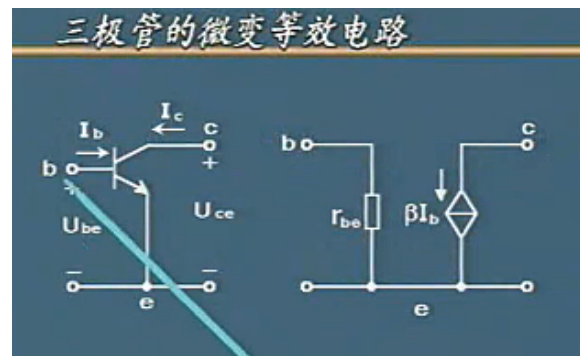
第二个问题 微变等效电路法

在放大电路的交流通路中用三极管的微变等效电路取代三极管，就得到放大电路的微变等效电路。

先看交流通路的基本共设放大电路。

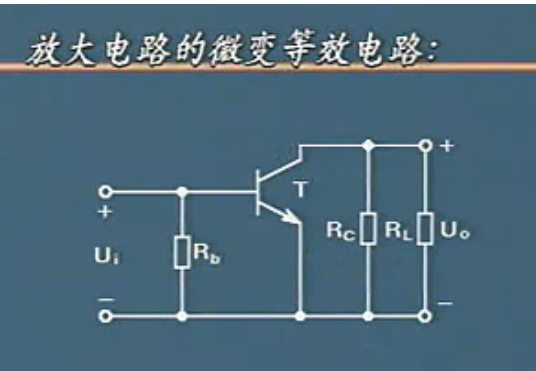
如果用微变等效电路取代的话就得带如下的图

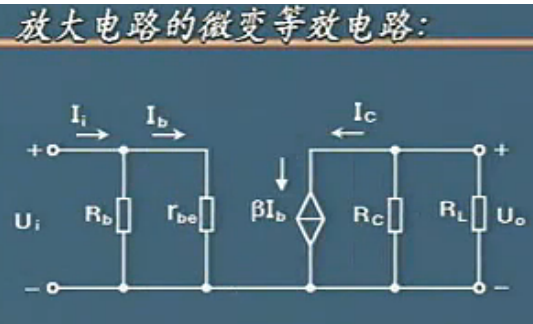
用微变等效电路可以求解动态参数Au Ri Ro

Ri表示放大电路的输入电阻

Ro是放大电路的输出电阻

1 求解放大倍数

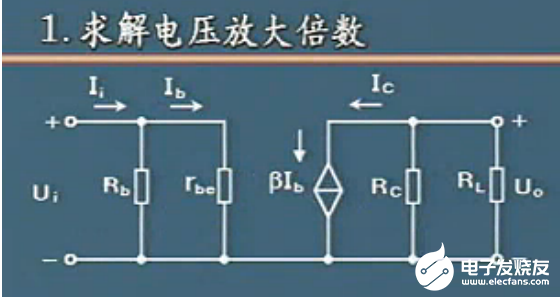
放大倍数的物理意义是

用输出电压÷输入电压等于Au

Ui=Ib*rbe

Uo=-βIb（Rb//Rc）负号表示相反

可以得到Au的表达式

2 求解输入电阻

当加入一个动态的电压Ui得到一个动态的电流Ii可以得到Ri

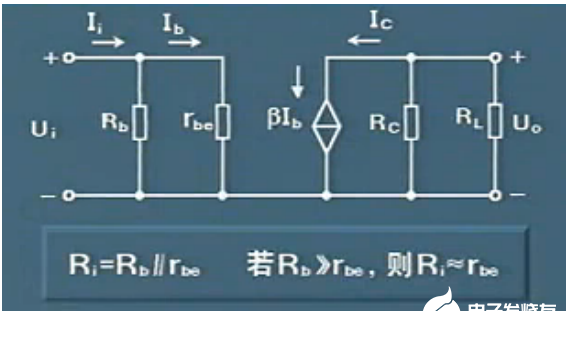
由上图可以看出输入电阻是决定于rbe那么输入电阻和Q点有紧密的关系

• 1放大电路的电压放大倍数增大则需要使Q点升高。
• 2 如果需要使输入电阻增大就要使得Q点降低。

求解输出电阻

输出电阻求解更具罗庚定理可以对电路图做如下简化

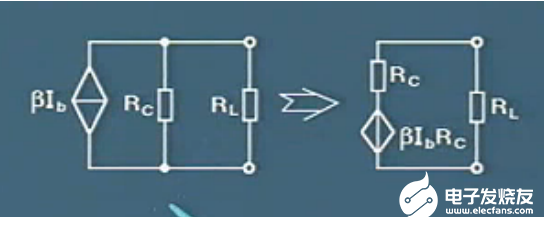
由上图可以看出基本共设放大电路的内阻Ro等于Rc

Ro = Rc

输出电阻还带啦一个负载电阻Rl，所以负载上加载的电压会被内阻Rc分区一部分，所以当Rc过大的时候负载能力就会降低，在分析放大电路的时候应当征询的一般规则：先静态后动态

放大电路的分析步骤

• 画直流通路
• 估算静态工作点
• 画微变等效电路
• 估算动态参数
• 失真分析