非对称密钥RSA加密算法及其密钥产生

一、 RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和 *** 作。 RSA是被研究得最广泛的公钥算法，从提出到现在已近二十年，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。RSA的安全性依赖于大数的因子分解，但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何，而且密码学界多数人士倾向于因子分解不是NPC问题。RSA的缺点主要有：A)产生密钥很麻烦，受到素数产生技术的限制，因而难以做到一次一密。B)分组长度太大，为保证安全性，n 至少也要 600 bits以上，使运算代价很高，尤其是速度较慢，较对称密码算法慢几个数量级；且随着大数分解技术的发展，这个长度还在增加，不利于数据格式的标准化。目前,SET(Secure Electronic TransacTIon)协议中要求CA采用2048比特长的密钥，其他实体使用1024比特的密钥。

　　（1）：随机选取两个100位(指十进制)以上的素数p和q；

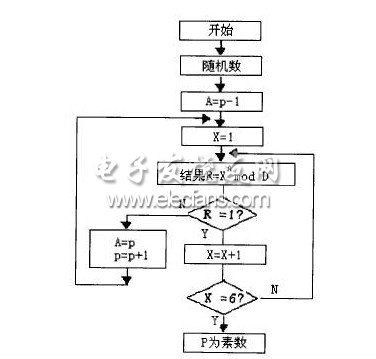
         产生素数的方法：根据修改的欧拉定理，如p为素数，则对于X的所有整数值，应满足:pow（X，（p一1））=1modP。

       这是一个必要条件而非充分条件，不过，如果有5个以上的X值能满足上述条件，则P可基本断定为素数。图1是产生素数的流程图，该流程图表示，如果X从1一5之间变化时，均能满足上述条件，则P为素数，否则将P十1，重复计算，直到获得素数为止。由此求得p和q，其乘积即为n。