一种多传感器可信度的确定方法

 

　　本文借鉴层次分析法(AnalyTIc Hierarchy Process，AHP)中分层的思想，提出了一种确定多个传感器可信度的方法，根据信息的相对可信度，建立了多传感器可信度的判断矩阵，该矩阵的正交特征向量即为对应传感器的可信度。仿真结果证明，融合数据要优于各传感器的算术平均值(等可信度融合)。

　　1 加权平均的数据融合模型

　　设在K时刻系统有p个传感器，q个目标，对传感器i，目标j测量值为：mij(i=1，2，…，p;j=1，2，…，q)。按照加权平均的融合算法确定传感器i的可信度为ai(i=1，2，…，p)，则目标j的融合结果为：

　　

 

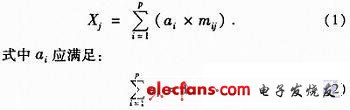
　　而ai(i=1，2，…，p)是需要确定的某时刻系统各传感器可信度。

　　2 层次分析法

　　T.L.Saaty于70年代提出层次分析法(AHP)，为解决多目标决策问题提供了很大的方便，在资源分配、企业管理、经济分析与计划、社会学、行为学中得到了广泛应用。其核心思想：首先，把要解决的问题分层系列化，即根据问题的性质和要达到的目标，将问题分解为不同的组成因素，按照因素之间的相互影响和隶属关系将其分层类聚组合，形成一个递阶的、有序的层次结构模型，然后，对模型中每一层次因素的相对重要性，依据人们对客观现实的判断，给予定量表示，再利用数学方法确定每一层次全部因素相对重要性次序的权值，最后，通过综合计算各层因素相对重要性的权值。

　　2.1 AHP可信度的确定

　　在多传感器探测系统中，在某时刻系统对传感器量测的信任程度，称为该时刻该传感器的可信度，针对系统中的p个传感器，q个目标。传感器对各目标的量测共有p×q个。根据q个目标分为q组，对于同一目标的量测分在一组。对于目标j，设各传感器量测的平均值：

　　

 

　　式中：mij表示第i个传感器对j目标的量测。

　　两个传感器s和t对目标量测可信度的比值定义如式(4)。在已知真实值时，可用真值代替平均值。

　　

 

　　该矩阵是对称阵，即

，且对角线元素为1。由式(4)，传感器量测距离平均值mj越近，该结果同其他结果的可信度比值就会越高，则判断矩阵中相应元素就会越大。对于目标j，该传感器的可信度也将会越大。判别矩阵求解可信度的步骤为：