单片机关键技术基础详解（五）

　　单片机被广泛应用于工业控制，家电，消费电子，医疗电子，仪表测量等领域，为应广大初级电子工程师/单片机爱好者之需，电子发烧友网隆重策划整合推出《单片机关键技术基础详解》系列技术文章，以后会陆续推出其他章节，敬请广大工程师朋友继续关注和留意。应广大工程师网友对前面章节热烈反响，电子发烧友网会再接再厉为各位工程师网友推出更多技术精品系列文章，以飨读者。

　　参阅相关系列章节

　　单片机关键技术基础详解（一）

　　单片机关键技术基础详解（二）

　　单片机关键技术基础详解（三）

　　单片机关键技术基础详解（四）
 

　　一、单片机矩阵键盘原理与结构

　　

　　在矩阵式键盘中，每条水平线和垂直线在交叉处不直接连通，而是通过一个按键加以连接。这样，一个端口（如P1口）就可以构成4*4=16个按键，比之直接将端口线用于键盘多出了一倍，而且线数越多，区别越明显，比如再多加一条线就可以构成20键的键盘，而直接用端口线则只能多出一键（9键）。由此可见，在需要的键数比较多时，采用矩阵法来做键盘是合理的。

　　《1》确定矩阵式键盘上何键被按下介绍一种“行扫描法”。

　　行扫描法 行扫描法又称为逐行（或列）扫描查询法，是一种最常用的按键识别方法，如上图所示键盘，介绍过程如下。

　　1、判断键盘中有无键按下 将全部行线Y0-Y3置低电平，然后检测列线的状态。只要有一列的电平为低，则表示键盘中有键被按下，而且闭合的键位于低电平线与4根行线相交叉的4个按键之中。若所有列线均为高电平，则键盘中无键按下。

　　2、判断闭合键所在的位置 在确认有键按下后，即可进入确定具体闭合键的过程。其方法是：依次将行线置为低电平，即在置某根行线为低电平时，其它线为高电平。在确定某根行线位置为低电平后，再逐行检测各列线的电平状态。若某列为低，则该列线与置为低电平的行线交叉处的按键就是闭合的按键。

　　《2》确定矩阵式键盘上何键被按下介绍一种“高低电平翻转法”。

　　首先让P1口高四位为1，低四位为0，。若有按键按下，则高四位中会有一个1翻转为0，低四位不会变，此时即可确定被按下的键的行位置。

　　然后让P1口高四位为0，低四位为1，。若有按键按下，则低四位中会有一个1翻转为0，高四位不会变，此时即可确定被按下的键的列位置。

　　最后将上述两者进行或运算即可确定被按下的键的位置。

　　更多矩阵键盘的资料请访问https://www.elecfans.com/zhuanti/20111025226587.html

　　二、什么是格雷码

　　格雷码（Gray code），又叫循环二进制码或反射二进制码 在数字系统中只能识别0和1，各种数据要转换为二进制代码才能进行处理，格雷码是一种无权码，采用绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码，是一种错误最小化的编码方式

　　简介

　　因为，自然二进制码可以直接由数/模转换器转换成模拟信号，但某些情况，例如从十进制的3转换成4时二进制码的每一位都要变，使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它是一种数字排序系统，其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意两个相邻的数之间转换时，只有一个数位发生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。另外由于最大数与最小数之间也仅一个数不同，故通常又叫格雷反射码或循环码。

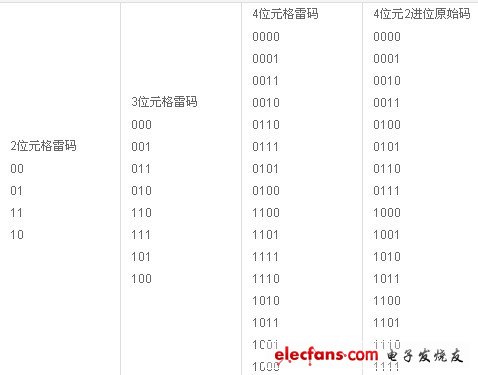
　　2、格雷码对照表

　　

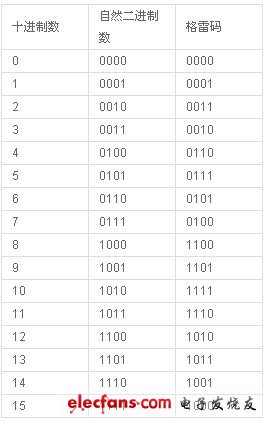
　　下表为几种自然二进制码与格雷码的对照表：

　　一般的，普通二进制码与格雷码可以按以下方法互相转换：

　　二进制码-》格雷码（编码）：从最右边一位起，依次将每一位与左边一位异或（XOR），作为对应格雷码该位的值，最左边一位不变（相当于左边是0）;

　　格雷码-〉二进制码（解码）：从左边第二位起，将每位与左边一位解码后的值异或，作为该位解码后的值（最左边一位依然不变）。

　　数学（计算机）描述：

　　原码：p［n:0］;格雷码：c［n:0］（n∈N）;编码：c=G（p）;解码：p=F（c）;

　　书写时按从左向右标号依次减小，即MSB-》LSB，编解码也按此顺序进行

　　编码：

　　。..。..。..。..。..。...c［n］=p［n］，

　　。..。..。..。..。..。...c［i］=p［i］ XOR p［i+1］ （i∈N，n-1≥i≥0）;

　　解码：

　　。..。..。..。..。..。...p［n］=c［n］，

　　。..。..。..。..。..。...P［i］=c［i］ XOR p［i+1］ （i∈N， n-1≥i≥0）。

　　Gray Code是由贝尔实验室的Frank Gray在20世纪40年代提出的（是1880年由法国工程师Jean-Maurice-Emlle

　　Baudot发明的），用来在使用PCM（Pusle Code ModulaTIon）方法传送讯号时避免出错，并于1953年3月17日取得美国专利。由定义可知，Gray Code的编码方式不是唯一的，这里讨论的是最常用的一种。

　　用异或乘除法实现二进制码与格雷码互相转换

　　如果在二进制运算中忽略进位、退位，那么加减运算都变成了异或（XOR）。

　　用异或代替加减进行二进制竖式乘除，称为异或乘除，它的特点是无进退位。

　　由于没有退位，异或除法将变得更像多项式除法。

　　如：10101除以11将变成1100余1，而不是111。

　　二进制转格雷码：

　　只要异或乘以二分之三，即二进制的1.1，然后忽略小数部分;也可以理解成异或乘以三（即11），再右移一位。

　　格雷码转二进制：

　　异或乘以三分之二，即除以1.1，忽略余数;或者左移一位，再异或除以三，忽略余数。

　　格雷码转二进制方法

　　二进位码第n位 = 二进位码第（n+1）位+格雷码第n位。因为二进位码和格雷码皆有相同位数，所以二进位码可从最高位的左边位元取0，以进行计算。（注：遇到1+1时结果视为0）

　　例如： 格雷码0111，为4位数，所以其所转为之二进位码也必为4位数，因此可取转成之二进位码第五位为0，即0 b3 b2 b1 b0。

　　0+0=0，所以b3=0

　　0+1=1，所以b2=1

　　1+1取0，所以b1=0

　　0+1取1，所以b0=1

　　因此所转换为之二进位码为0101

　　格雷码转换快速方法

　　（假设以二进制为0的值做为格雷码的0）

　　G：格雷码 B：二进位码

　　G（N） = B（n+1） XOR B（n）