一种用于FPGA的改进算法弱化了方波重影

　　0 引言

　　DDS（Direct Digital Frequency Synthesis）频率合成器能够很方便地输出任意波形，方波作为最常用波形之一，具有其特殊性。但输出的方波存在明显的重影现象直接影响了方波的质量。

　　1 方波重影出现的原因

　　假设系统时钟频率为200 MHz，以输出3 MHz方波为例，从模拟示波器观察到的结果如图1所示。

　　

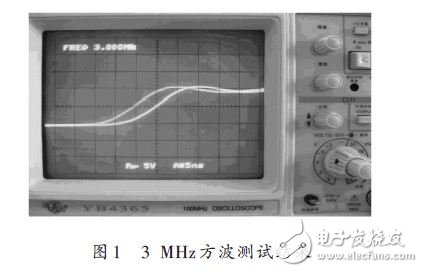
　　图1中存在明显的双边沿现象，且两条上升沿的间距为5 ns，刚好等于系统时钟的周期。这种现象可称为方波重影。

　　根据DDS的工作原理可知，相位序列具有周期性。

　　在相位序列的一个周期内，相位累加器会溢出若干次，并且每次溢出后的残留量都不一样。当残留量足够大时，再次发生溢出所需的累加次数会减少一次。累加次数的减少，意味着方波的周期变小。不同周期的方波叠加在一起，便出现重影现象。

　　使用Matlab模拟DDS生成方波的过程，可以得到更直观的认识，如图2所示。

　　

　　按照图2中的参数设置，方波的周期等于：

　　

　　从图2可以看出，为了输出周期为3.2Tc 的方波，在相位序列的一个周期内，DDS 频率合成器的实际输出为：一个周期为4Tc 且占空比为50%的方波，两个周期为3Tc 且占空比为75%的方波，两个周期为3Tc 且占空比为25%的方波。从平均的意义上看，刚好组成周期为3.2Tc 且占空比为50%的方波。因此，DDS 频率合成器输出的方波不仅周期在波动，而且占空比也发生波动。

　　如果将DDS 频率合成器看成分频器，在满足奈奎斯特采样定理［4］的条件下，可以得出如下结论：输出正弦波等连续信号时，DDS可以实现任意比例的分频；输出方波等存在跳变沿的信号时，这类信号的周期只能是系统时钟周期的整数倍，否则出现重影。

　　2 方波改进算法的研究与实现

　　为了解决方波重影问题，可从时域的角度分析。将若干个不同周期的方波叠加到一起，可得示意图如图3所示。

　　

　　图3 中，使a 点和d 点向下抖动，使b 点和c 点向上抖动，多次叠加后可有效弱化方波重影，甚至彻底消除。但是，如何准确地判断a、b、c、d 四个点，成为实现这一方法的最大障碍。

　　仔细观察图3和图2，引入时钟节拍的概念，便能找到依据判断a、b、c、d四个点。首先，定义方波的周期和上升沿时刻，以50%占空比为例，这两个数值可分别表示为：

　　

　　其中，ceil表示朝正无穷方向取整，floor表示朝负无穷方向取整，均为Matlab运算符［5］。

　　当系统时钟的频率为200 MHz时，以输出3 MHz方波为例，计算结果如表1所示。

　　

　　类似于图3，3 MHz方波的示意图如图4所示。

　　

　　从图4 可以看出，a 点和b 点发生在时钟节拍为33的位置，c点和d点发生在时钟节拍为65的位置。当出现c点时，意味着本次方波的周期较小，下一个时钟节根据图3 的规律，在时钟节拍为grl 和gda 的位置，利用原始方波信号的高低电平信息，就能得到a、b、c、d四个点。假设DAC的位数为14位，方波改进算法的实现过程可分为以下三个步骤：

　　第一步，定义一个计数器，并以相位累加器的进位输出信号作为清零信号，即相位累加器每溢出一次，该计数器就清零一次。因此，该计数器的计数值就表示图4中的时钟节拍。

　　第二步，定义一个状态机，假设计数器的计数值为num，简化后的状态转移图如图5所示。

　　

　　状态RISE标记的时钟节拍是grl，处于此状态时，如果原始方波信号为高电平，便得到a点；如果原始方波信号为低电平，便得到b点。状态DOWN标记的时钟节拍是gda，处于此状态时，如果原始方波信号为低电平，便得到c点；如果原始方波信号为高电平，便得到d点。

　　第三步，定义一个随机变量random，random的变化范围是0~2 048，可通过11位m序列实现之。使用verilog语言的位拼接运算符［6］，在a 点和d 点将送给DAC 的数据定义为10 240 加random，即“{3‘b101，random}”;在b 点和c 点将送给DAC 的数据定义为4 096 加random，即“{3’b010，random}”。

　　3 测试与总结

　　使用新的方波算法后，可得测试结果如图6所示。

　　

　　对比图6和图1可以看出，方波重影的宽度从5 ns缩短至3 ns，并且上升沿呈实心状，不再由两条边沿组成。

　　另一方面，图6和图1中，方波的上升时间均为15 ns左右，这说明方波改进算法并没有导致上升时间的增加。