机器学习之决策树生成详解_技术

1.什么是决策树

决策树是一种基本的分类和回归方法，本文主要讲解用于分类的决策树。决策树就是根据相关的条件进行分类的一种树形结构，比如某高端约会网站针对女客户约会对象见面的安排过程就是一个决策树：

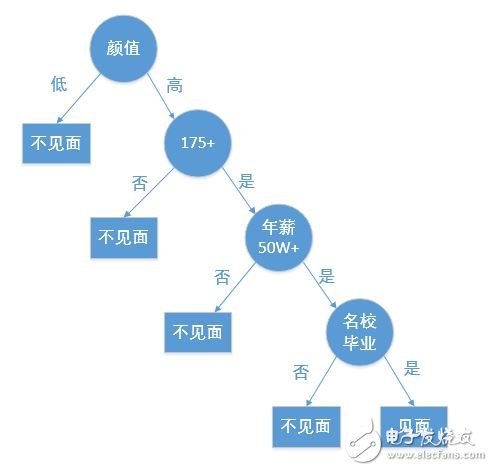
根据给定的数据集创建一个决策树就是机器学习的课程，创建一个决策树可能会花费较多的时间，但是使用一个决策树却非常快。

创建决策树时最关键的问题就是选取哪一个特征作为分类特征，好的分类特征能够最大化的把数据集分开，将无序变为有序。这里就出现了一个问题，如何描述一个数据集有序的程度？在信息论和概率统计中，熵表示随机变量不确定性的度量，即有序的程度。

现给出一个集合D，本文所有的讨论都以该集合为例：

序号不浮出水面是否可以生存是否有脚蹼是否为鱼类
1 是是是
2 是是是
3 是否否
4 否是否
5 否是否

创建该集合的代码如下：
def create_data_set():
dataSet = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels = ['no surfacing', 'flippers'] #不浮出水面是否可以生存，是否有脚蹼
return dataSet, labels

2.熵，信息增益和信息增益比

2.1熵(entropy)

博主第一次接触“熵”这个字，是在高中的化学课上，但是感觉“熵”在化学课上的含义和信息论中的含义没什么区别，都是表示混乱的程度，熵越大，越混乱，比如一杯浑浊水的熵就比一杯纯净的水熵大。

在信息论和概率统计中，设X是一个取有限个值的离散随机变量，其概率分布为：

编写计算熵的函数，其中dataSet是建立决策树的数据集，每行最后一个元素表示类别：
def cal_Ent(dataSet): #根据给定数据集计算熵
num = len(dataSet)
labels = {}
for row in dataSet: #统计所有标签的个数
label = row[-1]
if label not in labels.keys():
labels[label] = 0
labels[label] += 1
Ent = 0.0
for key in labels: #计算熵
prob = float(labels[key]) / num
Ent -= prob * log(prob, 2)
return Ent

2.2信息增益(informaTIon gain)

信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。

当熵和条件熵中的概率由数据估计得到时，所对应的熵与条件熵分别称为经验熵和经验条件熵。

决策树选择某个特征作为其分类特征的依据就是该特征对于集合的信息增益最大，即去除该特征后，集合变得最有序。仍旧以给定的集合D为例，根据计算信息增益准则选择最优分类特征。

以X1表示“不浮出水面是否可以生存”，则

编写选择最佳决策特征的函数，其中dataSet是建立决策树的数据集，每行最后一个元素表示类别：
#按照给定特征划分数据集，返回第axis个特征的值为value的所有数据
def split_data_set(dataSet, axis, value):
retDataSet = []
for row in dataSet:
if (row[axis]) == value:
reducedRow = row[:axis]
reducedRow.extend(row[axis+1:])
retDataSet.append(reducedRow)
return retDataSet

#选择最佳决策特征
def choose_best_feature(dataSet):
num = len(dataSet[0]) - 1 #特征数
baseEnt = cal_Ent(dataSet)
besTInfoGain = 0.0
bestFeature = -1
for i in range(num):
featlist = [example[i] for example in dataSet] #按列遍历数据集，选取一个特征的所有值
uniqueVals = set(featlist) #一个特征可以取的值
newEnt = 0.0
for value in uniqueVals:
subDataSet = split_data_set(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEnt += prob * cal_Ent(subDataSet)
infoGain = baseEnt - newEnt #信息增益
if (infoGain > besTInfoGain):
besTInfoGain = infoGain
bestFeature = i
return bestFeature