变频系统群时延测量技术探讨

　　引言

　　群时延是描述传输系统相频特性的重要指标，其测量方法大致可分为矢网法和调制法两类。调制法又分为调幅(AM)和调频(FM)两种。在实际使用中，由于FM比AM具有更好的抗干扰特性，因此被广泛采用，本文也采用FM法。

　　群时延基本概念

　　群时延的提出是基于对传输系统相频特性的描述，是群信号通过线性或非线性网络后信号整体产生的时延，其数学表达式为

　　上式中，j (w)为系统的相频特性，ω为载波信号角频率。

　　在线性传输网络中，系统相频特性在整个频带内和频率成正比，在工作频带内群时延为一常数，这样的系统对信息能无失真传输，如图1所示。

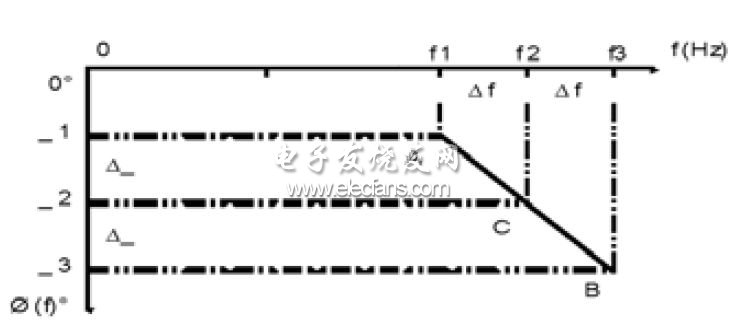
　　图1 线性网络相频曲线

　　但在实际应用中系统都不是理想系统，相频曲线上的不同位置具有不同的负斜率，如图2所示，

。

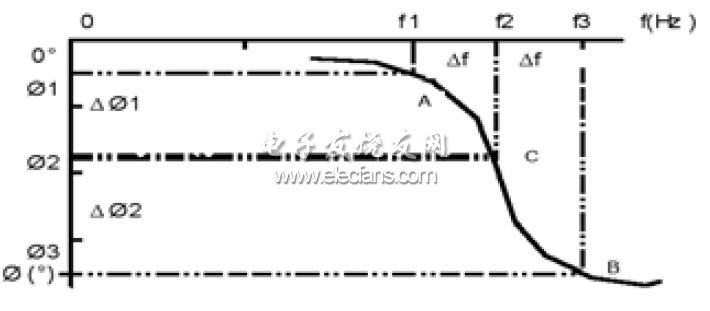
　　图2 非线性网络相频曲线

　　信号经过图2所示的系统后就会发生失真，这种系统通常被称之为非线性网络。

　　矢网法理论依据

　　矢网的测试方法基于群时延的定义，先测出传输系统的相频特性，然后再对相频曲线进行微分得出群时延。这种方法的测试精度由相位测量精度和“孔径”大小决定，相位测量精度越高，群时延测量精度也越高，同时孔径的选取也十分重要。所谓“孔径”实际上是群时延定义式中的分母部分。显而易见，在一定的相位测量精度下，选取较大“孔径”，能够有效改善群时延测量结果。但选取过大的“孔径”实际上又违背了群时延定义中的微分定义。本文根据安捷伦公司的资料提供，孔径最小值的取值方法为：测量的频率范围/(测量的频率点数-1)，也即选取相频曲线相邻两点做差分;孔径最大不得超出测量频率范围的20%。同时应该注意，选取“孔径”时，测量的两个频点之间的相位差不应大于180度。

　　调制法理论依据

　　不同频率的正弦波通过传输系统后，相位会发生不同变化，那这种变化对传输信号及信号所承载的信息会带来什么影响呢?考虑输入信号为：

.

　　其中，fc是载波中心频点，am(t)是低频调制信号，可以对载波进行调幅或调频。传输系统的幅频特性为：

　　其中，G(f)为传输系统的幅频特性，Q(f)为传输系统的相频特性。

　　经公式推导，合成信号的输出为：

　　其中af为每个频点对应的幅度，τc为载波的相位时延，τg为相频曲线上对应每个频点处的负斜率，即每个频点处的群时延。

　　对比(2)和(4)可以得出如下结论：已调制信号的群时延可以通过测试调制信号的时延得到。这一结论让我们可以用调制的方法测量传输系统的群时延。

　　也可以从另一方面来理解。对于一个信号来讲，真正有用的部分是信号所承载的信息，而信息都包含在调制信号中。如果在工作频带内调制信号的群时延是一常数，那么信息经过传输系统后，只是产生一个延迟，信息没有产生失真。反之，在工作频带内，调制信号的时延随着频率的变化有波动，所承载的信息就会发生失真。

　　应该指出的是，调制法在实际测量中是测调制信号经过传输网络前、后的时间差。这样一来，经过被测件后，解调出的低频信号质量就直接影响测量精度。