模拟电路之二阶系统之瞬态响应的设计

（文章来源：电力网）

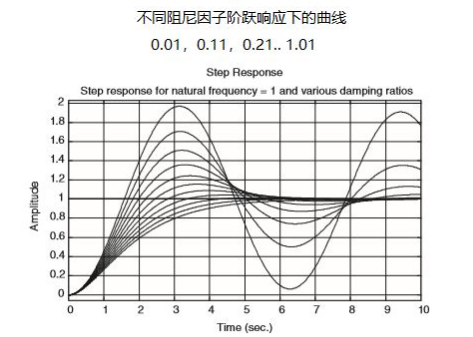
LCR二阶振荡系统，我们假设电阻足够小，系统处于欠阻尼状态，此系统有两个复平面极点。比如，对于阻尼因子为0.2的系统，振荡的峰值约为1.6倍。如果二阶系统增加一个或者多个极点，对系统有何影响？这取决于增加的极点离谐振频率ωn的远近。之前我们讲过，高频极点相当于幅值为1，负的相移-近似随频率的增加而减少（对应于时延）。

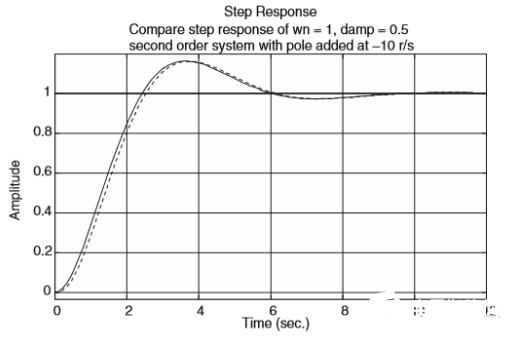
下图实线表示自然振荡频率ωn=1 radian/second, 阻尼因子ζ=0.5的阶跃响应曲线。虚线表示增加了额外高频极点-10 radian/second的阶跃响应曲线。可以看出这两个曲线基本重合，只是上升时间阶段，增加了额外极点的系统延时了0.1s，原因就是增加的高频极点带来的延时。

如果增加的额外极点位于-2 radian/second，增加了此极点的系统延时就比较明显了，原因是增加的额外极点的频率没有那么高。虚线就是增加了额外极点的阶跃响应曲线。由以上讨论可知，对于一个三阶振荡系统，如果最高频率是谐振频率的10倍以上，我们就可以忽略最高频率，系统可以等效成二阶振荡系统。
       （责任编辑：fqj）