模拟电路诊断中故障特征的提取方法

（文章来源：电子工程网）

故障特征提取是模拟电路故障诊断的关键，而模拟电路由于故障模型复杂、元件参数的容差、非线性、噪声以及大规模集成化等现象使电路故障信息表现为多特征、高噪声、非线性的数据集，且受到特征信号观测手段、征兆提取方法、状态识别技术、诊断知识完备程度以及诊断经济性的制约，使模拟电路的故障诊断技术滞后于数字电路故障诊断技术而面临巨大的挑战。模拟电路故障诊断本质上等价于模式识别问题，因此研究如何把电路状态的原始特征从高维特征空间压缩到低维特征空间，并提取有效故障特征以提高故障诊断率就成了一个重要的课题。

基于统计理论的特征提取

传统的基于统计理论的特征提取方法是考虑测点数据的一阶矩和二阶矩，根据这些测点数据的重要统计特征来降低特征空间维数达到有效特征提取的目的，其中包括基于可分离性准则、K-L变换、主元分析等特征提取方法。

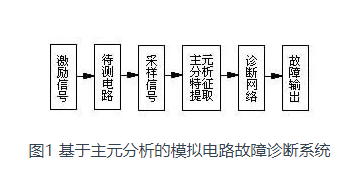
主元分析是基于数据样本方差－协方差（相关系数）矩阵的数据特征分析方法，它从特征有效性的角度，通过线性变换，在数据空间中找一组向量尽可能的解释数据的方差，将数据从原来的高维空间映射到一个低维向量空间，降维后保留数据的主要信息，且主分量间彼此独立，从而使数据更易于处理。在模拟电路故障诊断中，采用主元分析实现数据压缩和特征提取的过程是：首先将原始特征数据标准化，消除原变量的量纲不同和数值差异太大带来的影响；然后建立数据的相关矩阵，并计算矩阵的特征值及特征向量，并对所得的特征值进行排序。

基于统计理论的特征提取在应用中常常因为概率密度函数的分布问题使最优变换矩阵的计算陷入困境，而高分辨特征提取所需的映射常常是非线性的，因此基于统计理论的线性变换方法在使用时受到了限制。进一步的研究方向是其方法的非线性延伸，如非线性主元变换以及和其它特征提取方法的融合使用。

基于小波分析的特征提取

在电路信号的特征提取中，常采用频谱分析的方法。但是基于统计分析的傅立叶分析仅对不随时间变化的平稳信号十分有效，对于模拟电路响应信号中通常含有非平稳或时变信息却不能有效地提取故障特征。另外，模拟电路中含有大量噪声，若直接将高频成分当作噪声成份舍弃会造成有效成分的损失，若单纯对电路的输出进行分析，会导致故障模糊集较多，分辨率不高。而小波分析所具有的时频局部化特性、良好的去噪能力，无需系统模型结构的优势使之成为分析和处理此类信号的有效工具，也是目前在模拟电路故障诊断领域使用最多的一种特征提取方法，对模拟电路中的软、硬故障均适用。

小波分析的基本原理是通过小波母函数在尺度上的伸缩和时域上的频移来分析信号，适当选择母函数可使扩张函数具有良好的局部性，非常适合对非平稳信号进行奇异值分析，以区分信号的突变与噪声。目前在模拟电路故障诊断文献中用到了小波变换、小波包变换以及多小波变换等来对电路故障信息进行特征提取，对模拟电路瞬态信号的提取、消除电路噪声和模拟电路特有的元件参数容差具有良好的效果。

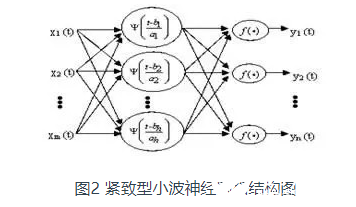
小波分析技术实现时与神经网络有两种结合方式：一是松散型结合，二是紧致型结合。松散型结构是数据预处理采用的最常见的方式，目前紧致型结构的小波神经网络也已成功用于模拟电路的去噪和特征提取。由于紧致型小波神经网络是用非线性小波基代替非线性的sigmoid函数，通过仿射变换建立小波变换与神经网络的连接，具有更强的逼近能力和收敛速度，不管是用于特征提取还是故障诊断都具有明显的优势。紧致型小波神经网络结构如图2所示。

小波分析技术中的多分辨率分析每次只对信号的低频部分进行分解，高频部分却保持不动导致了高频部分的分辨率很低。而小波包变换却提供了一种更加精细的分析方法，即可同时在低频和高频部分进行分解，以自适应地确定信号在不同频段的分辨率，使分解序列在整个时频域内都有较高的时频分辨率和相同带宽，更有效地进行特征提取。而多小波（MulTIwavelet）变换可以同时拥有对称性、正交性、短支撑性、高阶消失矩等重要性质，弥补了单小波的不足，也开始成为特征提取研究的热点。

小波分析在特征提取中的优势，主要是利用小波基可以用较少非零小波系数去逼近一类实际函数的能力，选择小波基应该是以最大量的产生接近于零的小波系数为优。小波基的这种能力主要依赖其数学特性――正交性、消失矩、正则性、对称性以及支集长度等来决定。在进行特征提取时选择不同的母小波，效果会有很大差异，而对于电路的特征分析中选择何种小波函数，目前还没有完善的理论指导，多根据经验或实验来确定，因此小波母函数、小波系数、小波网络结构及学习算法的优选问题都是亟待解决的问题。
      （责任编辑：fqj）