高敏感度SAW滤波器在无线数据测量中的应用

　　一个高效、精美的建筑物和能源管理系统应包括对业主电力、煤气和水进行自动记录的功能，这样不仅可降低成本、控制出错几率，还可免去费时的人工现场抄表作业。

　　先进抄表网络基础设施(AMI)系统用于记录用户数据，该系统通过无线电将数据传送到公共事业部门的网络中，再由能源管理系统对这些数据进行分析。收发机的灵敏性和选择性对于AMI和网络之间的可靠无线电连接至关重要。

　　通常有两种AMI系统：简单的单传系统和复杂的收发系统。传送机发送带有专门定时的数据，而收发机则只有在收到确认正确接收的单元所轮询后才发送数据。

　　SAW滤波器的优势

　　为保证可靠的数据传输，采用了各种各样的模块化方案。为此，作为一项规则，在多信道应用中，通常采用跳频展频(FHSS)或直接序列展频(DSSS)技术。比较而言，单信道应用时，则采用振幅偏移键控法(ASK)或频率键控(FSK)技术。AMI系统必须能够处理这些调制程序。另外，在实际应用中，还有来自其他无线射频的干扰，比如无线电话或业余无线电爱好者。因此无线射频前端必须具有高敏感度，以及很强的抗干扰能力。

　　现有的AMI系统使用SAW滤波器来抑制产生于IC的谐波和干扰发射信号。同时，它还可以保证高选择性。例如，在滤波器放置在天线后面或前面的AMI收发机的接收区域时。

　　与其它滤波方案相比，SAW滤波器具有一定的优势。例如，与LC滤波器相比较，即使是宽带SAW滤波器也具有更高的选择性、更低的插入损耗，因此其敏感度也更高(图1)。SAW滤波器的另一个优点是具有更低的温度系数。

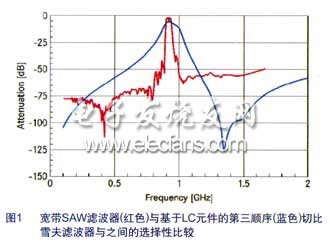
　　电路布局在AMI系统中的作用

　　对于LC和SAW滤波器而言，高选择性通常意味着高插入损耗和更低的敏感度。电路布局在AMI系统中起了关键的作用，这一点可以通过四项计算得以说明。在每个算式中，噪声因数F或更常见的对数噪声符号NF是衡量敏感度的参数。噪声因数指的是信噪电压比，它说明了与输出时该比率有关的四极元件的输入情况。公式如下：

　　F=\frac{S_{i}N_{i}}{S_{o}N_{o}}

　　或

　　NF=10log(F) (1)

　　其中：

　　Si：输出时的信号;So：输入时的信号;Ni：输入时的噪声;No：四极输出时的噪声。如果有两个以上的四极元件，可通过下列公式计算总噪声系数F1-n：

　　F_{1-n}=F_{1}+\frac{F_{2}-1}{G_{1}}+\frac{F_{3}-1}{G_{1}G_{2}}+…+\frac{F_{n}-1}{G_{1}G_{2}…G_{n-1}} (2)

　　其中：

　　n：四极数目;Fn：噪声因数;Gn：n个四极的增益因数。

　　直接安装在天线后面的第一个四极起了关键的作用。原则上说，它的噪声系数界定了总噪声系数的范围。

　　为简便起见，在相应的开关布局举例中，总噪声系数的计算中忽略了传送/接收(Tx/Rx)开关或平衡-不平衡转换器。在这些举例中，SAW滤波器的插入损耗IL、增益G、LNA以及接收机IC的噪声系数NF和噪声因数F均具有同样的值。同时，假设SAW滤波器的增益与其损耗相符，并假定它的噪声系数为其IL的负值。

　　所有四个例子的参数条件如下：

　　L_{SAW}=G_{SAW}=−2.9dB

　　G_{SAW(Linear)}=0.513

　　NF_{SAW}=2.9dB→F_{SAW}=1.95

　　G_{LNA}=15dB

　　G_{LNA(Linear)}=31.62

　　NF_{LNA}=1.5dB→F_{LNA}=1.41

　　NF_{RxIC}= 8dB，NF_{RxIC(Linear)}= 6.31

　　这四个例子各有优缺点。在例4中，总噪声系数是5.37 dB， 因此它的配置是基于无线射频AMI系统的最佳解决方案。它的特点是敏感度和选择性更高，再加上由于与第二个SAW滤波器对称工作，共模抑制率得以改善。