
本文给出了数字化宽带测向系统模型,讨论了数字化相位差测量方法,推导了数字化相位测量的数字化方法误差函数和由通道噪声引起的信号相位误差分布密度函数。相位差测量的精度直接影响系统测向的精度,还会影响解相位差模糊和天线阵列基线设置等一系列系统设计问题。传统的相位差测量方法都是利用窄带信号干涉原理把相位差转化为幅度进行测量的,因而其只能够适用于窄带信号的相位差测量,且测量精度受幅度测量误差的影响较大。本文提出的数字化相位差测量方法,其基本思想是把信号转换到频率域,利用信号的相位谱直接完成在给定频率点上相位差的测量,且全面的分析了相位差测量误差。
1 数字化宽带测向系统模型
数字化就是将许多复杂多变的信息转变为可以度量的数字、数据,再以这些数字、数据建立起适当的数字化模型,把它们转变为一系列二进制代码,引入计算机内部,进行统一处理,这就是数字化的基本过程。解释二:数字化将任何连续变化的输入如图画的线条或声音信号转化为一串分离的单元,在计算机中用0和1表示。通常用模数转换器执行这个转换。当今时代是信息化时代,而信息的数字化也越来越为研究人员所重视。早在40年代,香农证明了采样定理,即在一定条件下,用离散的序列可以完全代表一个连续函数。就实质而言,采样定理为数字化技术奠定了重要基础。英文digit译成“数字”是大陆的译法。最开始是不是由原信产部的研究所科研人员这样译出,尚不可考,愿有心有力者相助查寻。
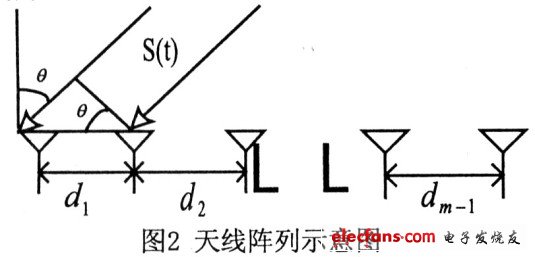
非均匀线阵的天线数为m,天线的间距分别为d1,d2,L dm-1宽带入射信号分别为s(t),入射方向与阵列法线的交角分别为θ。
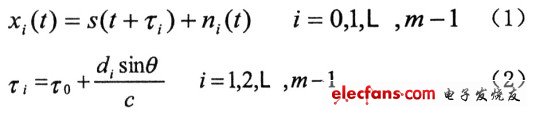
其中τ信号在第i个天线上相对于第O个天线的时间延迟,c是光速常数,di(l=1,2,L,m一1)为天线间距。对式(2)两边同做傅立叶变换:
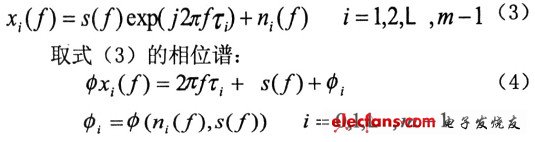
式(4)中φs(f)表示信号s的相位谱;φi为由噪声谱对信号相位谱影响产生的误差。作如下的相位差变换:

式(6)中相位差△φxi(f)是无模糊的相位差。然而实际中由于天线阵列的间距大于半波长因而相位差是有模糊的。
不妨令:

式中bi是有模糊的相位差,ni表示模糊整数,ai为相对基线长度,ei为相位差误差。则式(6)可代换为:
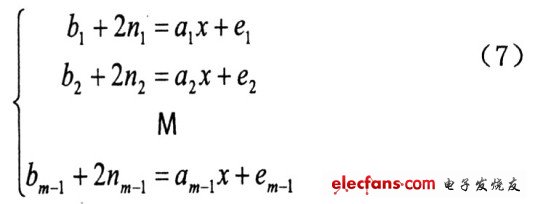
这是数字化宽带测向系统模型。
以下的工作都是围绕这个模型展开。其一是如何测量相位差bi(i=1,2,L,m一1) 及推导相位差测量误差ei(i=l,2,L,m一1)的分布密度函数。其二是如何快速求解模糊整数ni(i=1,2,L,m一1),即快速解模糊问题,这将在第二篇论文中讨论。其三是如何求解x的最优估计值从而获得测向角θ=arcsin(x),并进行测向角测量误差分析;同时还会讨论如何进行天线阵列的设计问题。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)