
盲源分离是指在信号的理论模型和源信号无法精确获知的情况下,如何从混迭信号(观测信号)中分离出各源信号的过程。盲源分离和盲辨识是盲信号处理的两大类型。盲源分离的目的是求得源信号的最佳估计,盲辨识的目的是求得传输通道混合矩阵。
1 引言
盲源分离主要分为线性混叠和非线性混叠两种。非线性混叠的主要有通过对线性模型的扩展和用自组织特征映射的方法[8]。
对于振动信号的盲分离,从2000年才开始受到重视[9],并且研究的范围主要在旋转机械和故障诊断中。
2 盲源分离基本概念
盲源分离问题可用如下的混合方程来描述[4]:
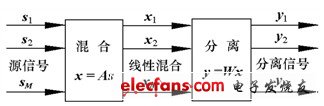
图1 线性盲源信号分离框图
事实上,在盲的范畴里,人们不可能实现源信号的完全恢复。盲源信号分离的求解结果有两个不确定性:分离后信号向量的排列位置可以变化、信号的幅值与初始相位可以变化。很明显,这样的不确定性对源信号的分离不会有任何实质的影响。
3 振动信号盲分离的常用算法
3.1 最大似然准则算法
最大似然估计是要找到矩阵W使得所估计的输出y的概率密度函数(PDF)与假设的源信号的PDF尽可能接近,是一种非常普遍的估计方法。
3.2 最小互信息准则及其算法
基于信息理论的最小化互信息的基本思想是选择分离矩阵W, 使输出y的各分量之间的互依赖性最小化,在理想情况下趋于零。
3.3 基于高阶累积量的方法
Cardoso提出了应用四阶矩进行盲信号分离的方法。在这个基础上,人们从度量的非高斯性出发,得到快速的定点盲源抽取算法。另外Tong和Liu通过正交变换,对观测到的混迭信号的四阶矩进行奇异值分解(SVD),得到一类扩展的四阶盲辨识和多未知信号提取算法。Cardoso还提出了基于四阶累积量的联合对角化。独立成份分析方法中的峭度与负熵也是基于高阶累积量的盲源分离方法。
3.4 非线性混叠盲源分离
大多数的盲源分离算法都假设混叠模型是线性的,更为准确的模型应当是非线性的或弱非线性的。人们针对非线性混叠模型提出了以下几种方法:(1) 基于两层感知器网络的感知器模型法[20];(2) 基于自组织特征映射的无模型方法;(3)径向基函数网络法,这种方法鲁棒性较好。
4 振动信号盲源分离方法的探讨
4.1 估计分离矩阵的加速梯度法
在最小化互信息准则的基础上,有关研究推导分析出加速梯度法的计算步骤,然后对转子的振动信号进行采集并盲分离,得到了满意的结果。
在一个转子试验台上安装2个加速度计和1个涡流传感器采集信号,得到的传感器信号与分离结果的功率谱,如图2和图3所示。
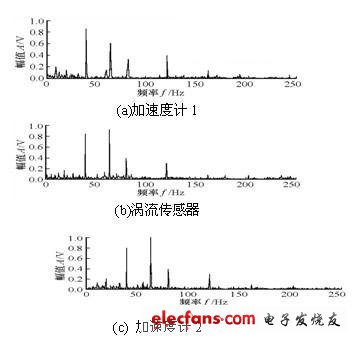
图2 各传感器采集的混合振动信号的功率谱
分析表明,基于最小化互信息原理的加速梯度法能够较好地估计出分离矩阵, 其实现步骤可行。
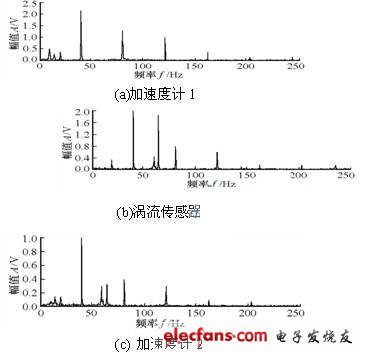
图3 分离后各传感器振动信号的功率谱
对具有故障的实际转子进行多传感器信号采集并进行盲分离,结果表明:采集信号中混叠的不同故障特征能够较好地分离开来,分离后各传感器信号的功率谱图基本上只显示出一种故障特征。但是旋转激励的影响不能从盲源分离的结果中完全消除。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)