通过各传感器数据同步提出的异质多传感器异步量测融合算法

1 引言

多传感器的集成与融合技术已经成为智能机器与系统领域的一个重要的研究方向。它涉及信息科学的多个领域，是新一代智能信息技术的核心基础之一。由于单传感器不可避免存在不确定或偶然不确定性，缺乏全面性，缺乏鲁棒性，所以偶然的故障就会导致系统失效。多传感器集成与融合技术正是解决这些问题的良方。多个传感器不仅可以描述同一环境特征的多个冗余的信息，而且可以描述不同的环境特征。多个传感器的使用还可以使信息采集和处理过程并行化，不仅可以得到更全面、更准确的信息，而且减少时间和成本，提高整个系统的性能。多传感器集成与融合的特点就是冗余性、互补性、及时性和低成本性。

本文从建立伪量测方程的角度，提出了一种异质多传感器的异步量测融合算法，该算法是通过在融合中心建立伪量测方程使各传感器的数据同步，然后利用同步的思想进行处理，最后通过计算机仿真进行了验证。

2 系统模型

不失一般性，以在球面坐标系中运动的目标为例进行分析，则离散时间线性系统的状态方程为：

X（k+1）=F（k+1，k）X（k）+Γ（k+1，k）V（k） （1）

其中，X（k）为k时刻目标的状态向量；kF（k+1，k）为状态转移矩阵；Γ（k+1，k）为过程噪声转移矩阵；V（k）是零均值，高斯白噪声序列，其协方差阵为Q（k）。

在实际情况下，传感器得到的是三维球坐标系或二维极坐标系的目标量测，即包括斜距r、方位角a和俯仰角e.假设某一传感器的测量方程为：

Z（k）=h（X（k））+W（k） （2）

其中，W（k）是k时刻的测量高斯白噪声，其相互独立且协方差为R（k），量测向量Z（k）包括斜距r（k）、方位角a（k）、俯仰角e（k），坐标转换如图2所示，由其定义可得：

3 测量方程的线性化

由于测量方程（2）是一个非线性方程，可以利用泰勒级数展开，对其进行线性化，展开围绕者预测状态X（k/k-1）进行，表示如下：

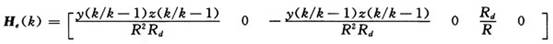
其中观测斜距用的量测矩阵Hr（k）由下式表示为：

故状态方程（1）和测量方程（4）组成线性化目标运动模型。

4 融合算法

假设采用N个传感器对目标进行观测，TI是第i个传感器的采样间隔，且在每个时间间隔［（k-1）T，kT］（T为融合周期）内各传感器共产生了Nk个量测，在该时间间隔内，某个传感器可能产生一个或几个量测，nik为传感器i提供量测的数目，则有：

若某个传感器j，在该时间间隔内没有提供量测，那么在式（5）中nik=0，这些量测在该时间间隔内是任意分布的。

令λik（i=1，2，…，Nk）为获得第i量测时间与KT之间的间隔，为方便标记，以下KT简写为K，如图2所示，则量测i的测量方程可表示为：

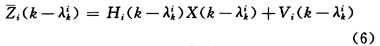
则单个融合间隔内的量测集合可表示为：

直到k时刻为止各传感器所有量测集合可表示为：

其中，Z（k），H（k），η（k）分别为扩维后的观测矢量、观测矩阵和测量噪声矢量，且有E［η（k）］=0，伪量测噪声之间的协方差矩阵为：

伪量测噪声与系统噪声之间的协方差矩阵为：

在条件1下，根据伪系统模型（1），（10），通过求解给定伪测量条件下关于目标状态的概率密度函数推导出相应的并行滤波异步数据融合算法：

则式（12）~（16）构成了异质多传感器扩维滤波融合算法，从中可知，该异步数据融合算法，计算较为简便，但其是在条件1下的滤波融合，故该算法在性能上为次优。

5仿真分析

假设采用雷达（测量值为斜距，方位角和俯仰角）和红外（方位角和俯仰角）2个传感器同时跟踪1个目标，设匀速直线运动目标的初始状态向量为x（0）=［30 000，-200，20 000，150，1 000，10］T，测量周期为T1=T2=2 s，传感器2比传感器1晚1 s开始采样，雷达和红外传感器的测距、测方位和测俯仰的精度为：σr=100 m，σa1=7 mrad，σa2=6 mrad，σe1=2 mrad，σe2=1 mrad，进行100次Monter Carlo仿真实验，采用滤波RMSE的均值Ps来度量各融合算法的估计精度，且：

仿真结果如图3所示。

6结语

本文提出一种不同传感器数据的融合算法，即首先是通过建立伪量测方程得到同步化的伪量测数据，之后利用一种扩维滤波的思想得到目标状态的最优估计，由于该算法适用与不同类型传感器异步数据的融合，所以该算法是一种实际算法。多传感器信息融合技术涉及到多学科、多领域，且具有多信息量、多层次、多手段等特点，并在机器人、故障诊断、图像处理等民用领域中，充分发挥了强大的信息处理优势，几乎一切需要信息处理的系统都可以应用信息融合，利用信息融合技术可得到比单一信息源更精确更完全的判断。在将来，多传感器信息融合技术以军事应用为核心，将不断地向工业、农业等领域渗透，进而取得更为广泛的应用。