
除了Clock之外,对于电路其他输出输入端点及其周边的环境(Boundary CondiTIon)也要加以描述。在说明Boundary CondiTIon之前,我们得对路径(Path)有更进一步的了解。上文曾提及STA会将电路中所有的Path找出来加以分析,但Path的定义是什么呢?
Path根据起点及终点可以分为4种:
由Flip-Flop Clock输入到Flip-Flop资料输入(图十七左上)。
由主要输入(Primary Input,简称PI)到Flip-Flop资料输入(图十七右上)。
由Flip-Flop Clock输入到主要输出(Primary Output,简称PO)(图十七左下)。
由主要输入到主要输出(图十七右下)。
当Clock规格确定了之后,第1种Path的时序限制(TIming Constraint)就自动的给定了。为了给定其他3种Path的时序限制,我们必须定义Boundary CondiTIon。
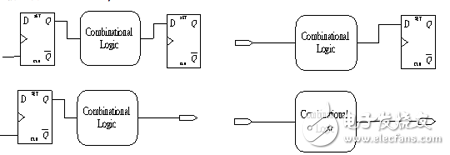
图十七
一般来说,我们会定义下列的Boundary Condition:
Driving Cell:定义输入端点的推动能力(图十八)。
Input Transition Time:定义输入端点的转换时间(图十八)。
Output Capacitance Load:定义输出负载(图十八)。
Input Delay:输入端点相对于某个Clock领域的延迟时间。(图十九,Delayclk-Q + a)
Output Delay:自输出端点往外看相对于某个Clock领域的延迟时间。(图十九,c)
在这些Boundary Condition定义之后,上述4种Path事实上都可看成是第1种Path(Flip-Flop到Flip-Flop)。也就是说,加上 Boundary Condition后,只要Clock给定,所有Path的Timing Constraint就会自动给定。
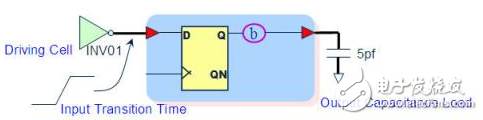
图十八
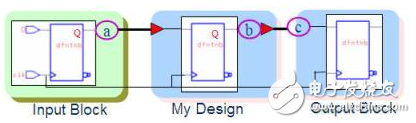
图十九
由于每个Path都有Timing Constraint,所以时序分析都能够进行。但在某些情况下,有些Path的分析可能没有意义,因此你会想忽略这些Path的分析。或是有些Path 分析的方式不一样,你会想指定这些Path的分析方式。此时就要设定一些Timing Exception,如False Path和Multi-cycle Path等等来处理非一般性的时序分析。
STA流程及分析方式
STA的流程如图二十所示,而其分析验证的项目就是我们前文提及之时序检查相关的Timing Arc,如Setup Time、Hold Time等等。以下我们针对Setup Time举1实际范例来说明STA的分析方式。
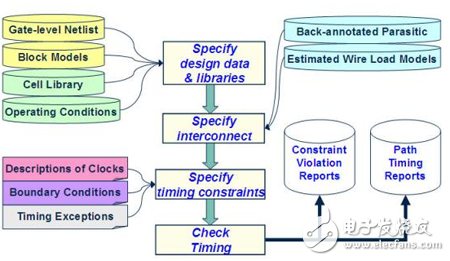
图二十
Setup Time
设计电路如图二十一所示,时序模型(Timing Model)及时序限制(Timing Constraint)如下:
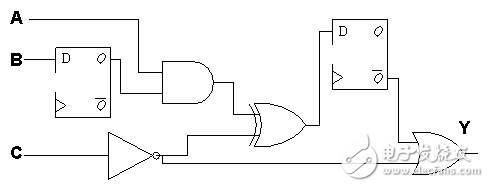
图二十一
所有逻辑闸在输出讯号上升时最长的延迟时间为3ns,最短为2ns。
所有逻辑闸在输出讯号上升时最长的延迟时间为2ns,最短为1ns。
所有连线(Net)最长的延迟时间为2ns,最短为1ns。
所有Flip-Flop Clock到Q的延迟时间为3ns。
所有Flip-Flop的Setup Time为1ns(Ts)。
所有Flip-Flop的Hold Time为1ns(Th)。
Clock周期为14ns(Dclkp)。
Clock source latency为2ns(Dclks)。
Clock network latency为3ns(Dclkn)。
Clock uncertainty为1ns(Dclku)。
B及C的input delay皆为1ns(Da、Db、Dc)。
Y的output delay为3ns(DY)。
接下来,我们以Step-By-Step的方式说明时序分析的方式。
1. 首先找出所有Timing Path,我们只列出具代表性的3条Timing Path来加以说明。
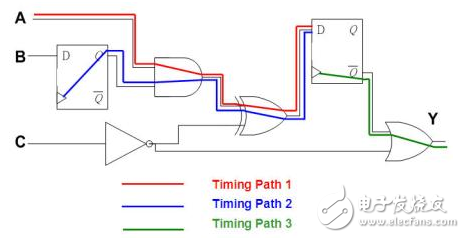
图二十二
2. 假设输入A讯号由0变1,计算第1条Path终点讯号到达的时间(Arrival Time简称AT)。
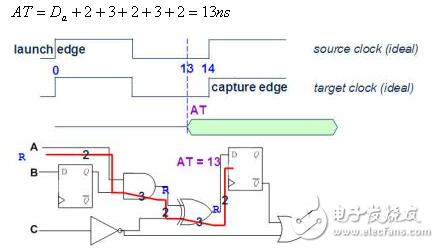
图二十三
3. 假设输入A讯号由1变0,计算第1条Path终点AT。
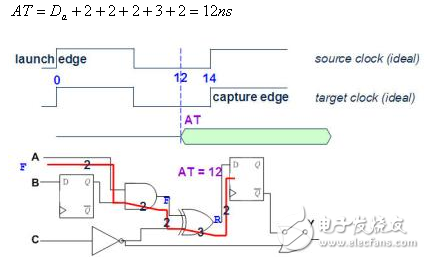
图二十四
4. 计算第1条Path终点的需求时间(Required Time,简称RT)。
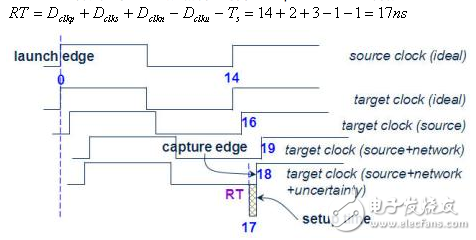
图二十五
5. 假设输入A讯号由0变1,计算第1条Path终点的Slack。Slack等于RT和AT的差值,对于Setup Time验证来说等于RT - AT,对于Hold Time验证来说等于AT - RT。在此Setup Time范例中,Slack为正,表示讯号实际到达Path终点时间比必须到达的时间还早,因此Timing是满足的。
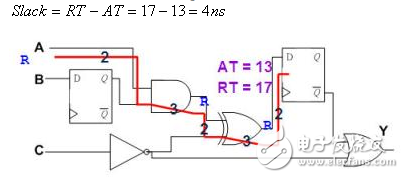
图二十六
6. 假设输入A讯号由1变0,计算第1条Path终点的Slack。Slack为正,因此Timing是满足的。
综合5和6,第1条Path的Timing是符合规格的,其Slack为4ns(取较差状况)。
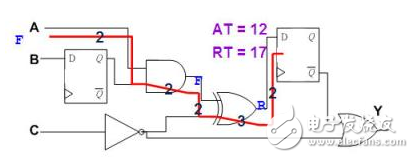
图二十七
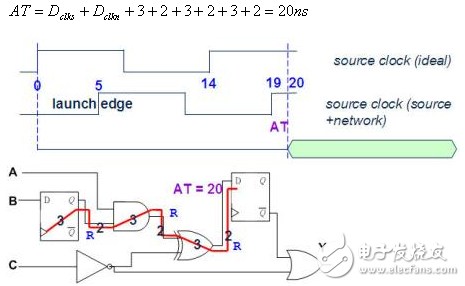
7. 假设前级Flip-Flop的讯号由0变1,计算第2条Path终点的AT。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)