全卷积网络FCN进行图像分割

CNN能够对图片进行分类，可是怎么样才能识别图片中特定部分的物体，在2015年之前还是一个世界难题。神经网络大神Jonathan Long发表了《Fully ConvoluTIonal Networks for SemanTIc SegmentaTIon》在图像语义分割挖了一个坑，于是无穷无尽的人往坑里面跳。

全卷积网络 Fully ConvoluTIonal Networks

CNN 与 FCN

通常CNN网络在卷积层之后会接上若干个全连接层, 将卷积层产生的特征图(feature map)映射成一个固定长度的特征向量。以AlexNet为代表的经典CNN结构适合于图像级的分类和回归任务，因为它们最后都期望得到整个输入图像的一个数值描述（概率），比如AlexNet的ImageNet模型输出一个1000维的向量表示输入图像属于每一类的概率(softmax归一化)。

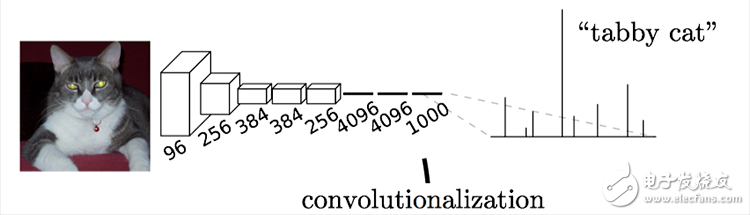
栗子：下图中的猫, 输入AlexNet, 得到一个长为1000的输出向量, 表示输入图像属于每一类的概率, 其中在“tabby cat”这一类统计概率最高。

FCN对图像进行像素级的分类，从而解决了语义级别的图像分割（semantic segmentation）问题。与经典的CNN在卷积层之后使用全连接层得到固定长度的特征向量进行分类（全联接层＋softmax输出）不同，FCN可以接受任意尺寸的输入图像，采用反卷积层对最后一个卷积层的feature map进行上采样, 使它恢复到输入图像相同的尺寸，从而可以对每个像素都产生了一个预测, 同时保留了原始输入图像中的空间信息, 最后在上采样的特征图上进行逐像素分类。

最后逐个像素计算softmax分类的损失, 相当于每一个像素对应一个训练样本。下图是Longjon用于语义分割所采用的全卷积网络(FCN)的结构示意图：

简单的来说，FCN与CNN的区域在把于CNN最后的全连接层换成卷积层，输出的是一张已经Label好的图片。

其实，CNN的强大之处在于它的多层结构能自动学习特征，并且可以学习到多个层次的特征：较浅的卷积层感知域较小，学习到一些局部区域的特征；较深的卷积层具有较大的感知域，能够学习到更加抽象一些的特征。这些抽象特征对物体的大小、位置和方向等敏感性更低，从而有助于识别性能的提高。下图CNN分类网络的示意图：

这些抽象的特征对分类很有帮助，可以很好地判断出一幅图像中包含什么类别的物体，但是因为丢失了一些物体的细节，不能很好地给出物体的具体轮廓、指出每个像素具体属于哪个物体，因此做到精确的分割就很有难度。

传统的基于CNN的分割方法：为了对一个像素分类，使用该像素周围的一个图像块作为CNN的输入用于训练和预测。这种方法有几个缺点：一是存储开销很大。例如对每个像素使用的图像块的大小为15x15，然后不断滑动窗口，每次滑动的窗口给CNN进行判别分类，因此则所需的存储空间根据滑动窗口的次数和大小急剧上升。二是计算效率低下。相邻的像素块基本上是重复的，针对每个像素块逐个计算卷积，这种计算也有很大程度上的重复。三是像素块大小的限制了感知区域的大小。通常像素块的大小比整幅图像的大小小很多，只能提取一些局部的特征，从而导致分类的性能受到限制。

而全卷积网络(FCN)则是从抽象的特征中恢复出每个像素所属的类别。即从图像级别的分类进一步延伸到像素级别的分类。

全连接层 -> 成卷积层

全连接层和卷积层之间唯一的不同就是卷积层中的神经元只与输入数据中的一个局部区域连接，并且在卷积列中的神经元共享参数。然而在两类层中，神经元都是计算点积，所以它们的函数形式是一样的。因此，将此两者相互转化是可能的：

对于任一个卷积层，都存在一个能实现和它一样的前向传播函数的全连接层。权重矩阵是一个巨大的矩阵，除了某些特定块，其余部分都是零。而在其中大部分块中，元素都是相等的。

相反，任何全连接层都可以被转化为卷积层。比如，一个 K=4096 的全连接层，输入数据体的尺寸是 7?7?512，这个全连接层可以被等效地看做一个 F=7,P=0,S=1,K=4096 的卷积层。换句话说，就是将滤波器的尺寸设置为和输入数据体的尺寸一致了。因为只有一个单独的深度列覆盖并滑过输入数据体，所以输出将变成 1?1?4096，这个结果就和使用初始的那个全连接层一样了。