基于FGPA实现数字下变频器的抽取滤波器设计方案详解

设计数字下变频器的抽取滤波器是一项艰巨任务。本文介绍一种能够完成此项任务的简便、易于理解的流程。

过去半年有几位客户请我帮助他们设计和实现数字下变频器所用的降采样（即“抽取”）滤波器，这种滤波器在软件无线电与数据采集类应用中都很常见。这项工作即便对于经验丰富的设计师也不是一件小事。事实上，仅仅算出在FGPA中实现滤波器所需要的资源可能就是一个很大的问题。虽然MATLAB®（MathWorks 开发）具有用于滤波器设计与分析 （FDA） 的绝妙工具箱，但是它提供太多滤波器设计方法，会让新用户无从下手。另外，您必须能够根据DSP理论解释MATLAB命令产生的结果，仅仅这一点就需要研究。

抛开理论的细枝末节，让我们开始围绕上述问题探讨降采样有限脉冲响应 （FIR） 滤波器的设计与实现。本辅导资料实际上旨在向您介绍一种简便、易于理解的流程——从滤波器系数生成到FGPA目标器件中抽取滤波器的实现。所需工具只有MATLAB较新版本（本人仍在使用R2008a）及其FDA工具箱、以及ISE® 11.4套件提供的赛灵思CORE GeneratorTM工具。这些工具是设计多速率FIR滤波器的必备工具。

特别是我们将探讨固定降采样速率变化的两个实例：整数值与有理值。您应当能够把我们在本辅导资料介绍的MATLAB指令和CoreGen图形用户界面 （GUI） 设置应用到您的设计当中。为了说明公用逻辑块 （CLB） Slice 、18KB内存RAM块（BRAM） 和DSP48乘法累加 （MAC） 单元等方面的资源占用情况，我们将采用 XC6VLX75T-2ff484 作为目标 FPGA 器件。

整数倍降采样器假设基带中进行解调后按250MHz速率传输带宽只有2.5MHz的信号。我们必须过滤从2.5MHz到 250MHz 的所有频率，因为它们不传输任何有用信息；这正是我们准备设计和实现的低通 FIR 滤波器的目的。根据尼奎斯特定理，输出数据速率是信号带宽的两倍；因此，我们需要按照M=50的整数倍对其执行降采样。我将介绍两种采用多级滤波方法的可行备选实现方案：第一种方法采用三个串联的 FIR 抽取滤波器，而第二种方法则同时采用级联积分梳状 （CIC） 滤波器与FIR滤波器。

以下是用于设计理想滤波器的MATLAB代码。我们假设通带和阻带频率的衰减分别为0.1dB和100dB。

假设FPGA时钟频率Fclk=Fs_in，那么在Virtex®-6器件中我们需要多少个DSP48 MAC单元？它是用于按M进行降采样的滤波器。根据FIR Complier 5.0数据手册 （fir_compiler_ds534.pdf） 详细阐述的理论，我们可以把DSP48 MAC分成M个相位，因此引入“多相”这一术语。由于每个相位都是按更低的输出频率 Fs_out 进行处理，因此可以按时分复用方式共享DSP48 MAC。以下理论计算表明，FIR-Compiler在通过多相分解方式实现滤波器时采用最小的22个MAC单元（total_num_MAC_ref ）。滤波器长度是2100 （total_num_coeff），填写0成为M的整数倍。请注意：此方案考虑系数对称性。

在MATLAB中可以轻松按低通滤波建立抽取过程模型，然后按M降采样，最终分别产生y与y_filt输出信号。不过，在FPGA器件中，这种实现方式效率不高：它会很笨地计算随后必须抛弃的值。相反，多相抽取器把输入信号降采样到M个wk通道，每个通道由其自身的子滤波器ph（k，：） 过滤。部分结果y_out（k，：） 然后汇总在一起组成最终输出y_tot。把y_tot与本机MATLAB指令产生的基准 y 对比，结果表明最终输出均处于数值精度3e-15范围内（由于不同运算阶数而出现偏差）。

为了设计参考滤波器，CoreGen FIR-Compiler需要名为“COE 文件”的系数文本文件。以下MATLAB例程说明如何以十进制基数轻松生成此 COE 文件；FIR-Compiler 然后按照所采用的设置量化相关系数。

图1与图2说明FIR-Compiler GUI头两个页面所应用的设计参数；在最后两个页面我只需接受其默认值，但是“优化目标 （OpTImizaTIon Goal）”除外， 我把它设为“速度 （Speed）”而非“区域 （Area）”。如无明确说明，我在本文件以及下面例子中始终采用上述设置。在完成ISE 11.4布局布线之后，参考单级降采样滤波器占用以下FPGA资源：

Slice触发器数量：1，265 个

Slice LUT数量：1，744 个

占用的 Slice数量：502 个

DSP48单元数量：22 个

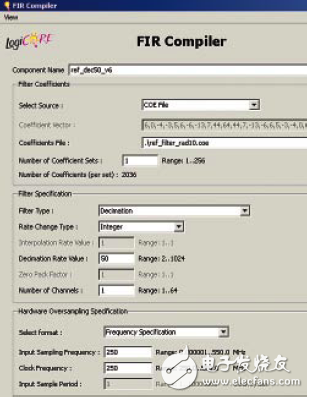
图 1. 50整数降采样 

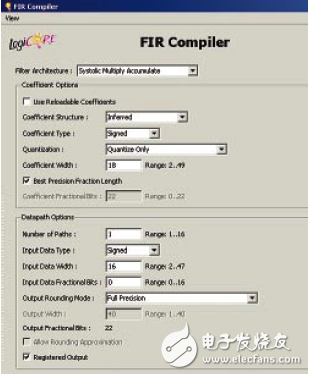
图 2. 50整数降采样 

三个FIR滤波级串联

现在我们以滤波级串联方式实现理想抽取滤波器。这种方法可以让我们通过时分复用节省MAC单元，因为每个新的滤波级都是按前一级提供的较低数据速率运行。我让FDA工具决定最佳滤波类型：利用 MATLAB 指令信息，您可以看出：它会提出三级解决方案建议，其抽取因数分别是M1=2、M2=5和M3=5。

图3显示了组成上述多级系统的三个滤波器的频率响应。蓝色曲线代表第一个降采样滤波器（M1=2）；绿色曲线代表第二个滤波器 （M2=5），按Fs_in/M1倍数周期波动；而红色曲线则代表第三个降采样器 （M3=5），按Fs_in/（M1*M2）倍数周期波动。

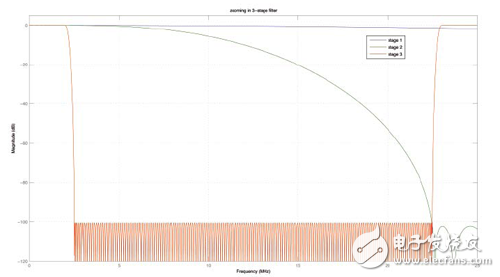
图 3. 通过串联三个FIR滤波级进行的按 50 整数抽取，此处单独放大显示0~25MHz频率。

用于三级滤波器的FIR-Compiler设置与图1及图2所示大同小异。第一个滤波器唯一不同的参数是COE文件名和“抽取率值”，其分别设为filt1_rad10.coe和M1=2。第二个滤波器COE文件名是filt2_rad10.coe，抽取率值为M2=5，输入采样频率此时为125MHz，因为第二级按M1=2抽取来自第一级的输入数据。最后，第三个滤波器参数的唯一区别是COE文件名为filt3_rad10.coe，抽取率值为M3=5，输入采样频率此时为25MHz，因为第三级按M2=5抽取来自第二级的输入数据。

在布局布线后，三个滤波级占用以下FPGA资源：

第一级（M1=2）：

Slice触发器数量：280 个

Slice LUT数量：208 个

占用 Slice数量：62 个

DSP48 MAC单元数量：3个

第二级（M2=5）：

Slice触发器数量：236个

Slice LUT数量：168 个

占用 Slice数量：60 个

DSP48 MAC单元数量：3 个

第三级（M3=5）：

Slice触发器数量：357 个

Slice LUT数量：414 个

占用 Slice数量：158 个

DSP48 MAC单元数量：4 个

由于采用上述多级方法，我们现在比参考滤波器最初的22个DSP48 MAC单元少用了12个单元；与单级理想滤波器占用资源相比，我们节约了30%左右的触发器，55%的LUT，44%的slice和54%的DSP48单元。

与CIC滤波器串联

另一种按50抽取的可行方法是把级联积分梳状 （CIC） 滤波器 和CIC补偿降采样级串联在一起，其变化速率分别为M1=10与M2=5。CIC滤波器是一类特殊的FIR滤波器，由N个梳状滤波器和积分器组成（因此产生“第 N 级”术语）。尽管梳状滤波器仍然可以实现成一种“传统的”基于MAC的FIR滤波器，不过CIC架构之所以有趣是因为它不需要任何MAC单元，因此可以用CLB sclice替代DSP48单元，参阅CoreGen CIC-Compiler 1.3数据手册（cic_compiler_ds613.pdf）。

按M1=10抽取的第一级CIC滤波器频率响应较差，因此需要采用一个按M2=5抽取的补偿FIR滤波器，以弥补第一级CIC滤波器本身通带的下降。以下MATLAB代码说明如何采用FDA工具设计此类滤波器。

图4为赛灵思CoreGen CICCompiler 1.3 GUI设置的第一个页面；其它参数采用默认值，“使用Xtreme DSP Slice”可选参数除外 

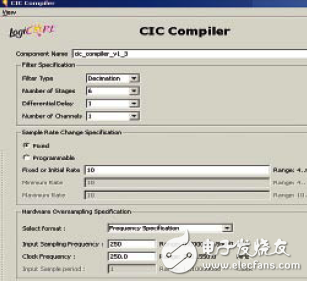
图 4. 按10抽取的CIC滤波器的设置 

其允许采用或不采用DSP48单元实现梳状滤波器。FIR Compiler GUI中的CIC补偿FIR滤波器设计参数与图1及图2所示相同；唯一不同的设置是 COE 文件名（此处是ciccomp_ dec5.coe），抽取率值为M2=5，而输入采样频率为25MHz。

在布局布线后，两个滤波级占用以下FPGA资源：

第一级（按10抽取的CIC滤波器，不使用“采用Xtreme DSP Slice”）

Slice 触发器数量：755 个

Slice LUT 数量：592 个

占用 Slice 数量：172 个

DSP48 MAX 单元数量：0 个

第一级（按10抽取的CIC 波器，使用“采用 Xtreme DSP Slice”）

Slice 触发器数量：248 个

Slice LUT 数量：154 个

占用 Slice 数量：42 个

DSP48 MAC 单元数量：7 个

第二级（按5抽取的CIC补偿FIR滤波器）

Slice 触发器数量：271 个

Slice LUT 数量：312 个

占用 Slice 数量：114 个

DSP48 MAC 单元数量：3 个

两种结果都很有趣，而是否选择使用Xtreme DSP slice取决于设计人员最需要节约哪些资源。我个人选择“采用Xtreme DSP Slice”选项。与单级滤波器相比，我们可以节约大约59%的触发器，73%的LUT，69%的slice和54%的DSP48 MAC单元。代价是阻带衰减更差，其现在是80dB，而非所需要的100dB，如图5所示。某项设计是否接受该衰减值事实上与应用相关。

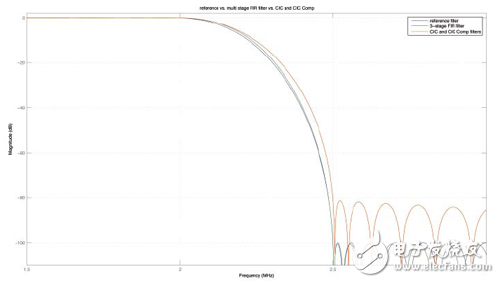
图 5. 三个降采样器的频率响应 - 整体速率变化为50，图中显示了放大的1.5~3MHz频段。单级滤波器为蓝色，三级滤波器（比例分别为M1=2、M2=5、M3=5）为绿色，基于CIC的二级滤波器（比例分别为M1=10、M2=5）为红色。

图5对比上述三种按50降采样方法：单级、三级（比例为 2-5-5）和CIC滤波器与CIC补偿FIR滤波器串联（比例为10-5）。

有理数降采样

在此第二个应用示例中，我们假设信号输入数据速率是50MHz，其必须降采样到12MHz，因此其需要采用L/M=6/25 的有理数固定速率变化（换句话说，抽取因数为M/L=25/6）。FPGA时钟频率假设为150MHz。

如FIR-Compiler 5.0数据手册所解释，采用有理数速率变化的滤波器理论上需要两个处理步骤：按L插值，然后是按M抽取。在我们这个具体例子中，一旦输入信号按L=6插值，输出虚拟采样速率 Fv 就会变为300MHz。因此，必须过滤掉Fs_in/2=25MHz与Fv/2=150MHz之间的频段，以滤除Fs_in整数倍之处的频谱。在DSP术语中其称为“图像”，这正是采用插值“抗成像”低通滤波器的原因。

在上述处理步骤之后、按M最终降采样之前，我们需要采用低通滤波器滤除从Fv/（2*M）=6MHz到Fv/2=150MHz的频率，其在DSP术语中称为“混叠”。由于这两个低通滤波器是串联在一起并且按相同的虚拟数据速率Fv运行，因此我们可以使用带宽较低的滤波器同时执行抗成像与抗混叠，从而节约资源。在我们的例子中，具有最低带宽的滤波器是抽取滤波器。

以下MATLAB片段说明如何使用单级滤波器设计和模拟上述降采样器。我们假设通带和阻带频率衰减分别为0.05dB和70dB。

请注意：此MATLAB代码只是有理数降采样滤波器的行为模型。在实际硬件多相架构中，您只需实现一个单相滤波器，然后改变每个新输出采样的系数即可（按Fclk速率执行处理）。其不同于采用整数比的多相降采样滤波器。

图6说明FIR-Compiler GUI第一个页面的设置。其它三个页面本人采用与第一个整数降采样应用例子相同的参数。布局布线后的总体FGPA资源占用情况如下：

Slice触发器数量：547 个

Slice LUT数量：451个

占用 Slice数量：153个

DSP48单元数量：13

BRAM单元数量：6个

图 6. 25/6有理数降采样 

多级方法

FIR-Complier已经为这种多相L/M=6/25滤波器生成了非常小的内核。不过，我们需要再次采用多级方法，因为这种方

法使我们能够进一步节约DSP48与BRAM。在手动设计多级系统时， 如本例所示，所有滤波级都必须采用与参考滤波器相同的通带频率 （Fpass）。

各级通带纹波均相等，是由参考滤波器通带纹波除以级数算出。各级的差异是阻带频率。第一级无需在Fstop截止，因

为转换带宽会变得太急促（太多系数）；现实中我们所需要的只是让第一级在Fstop1=Fs_in/M1- Fs_in/（2M/L）截止。实际上Fs_in/M1与其所有倍数此时都是放置所有复本的新采样频率，而Fs_in/（2*M1）是Fs_in/M1中第一个复本的带宽的一半。以下是相关MATLAB代码。

由于第一级是M1=4整数降采样器， 因此其FIRCompiler GUI设置与图1所示非常相似。唯一不同的参数是COE文件名（即dec_L1_M4_rad10.coe）、抽取率值（M1=4）、输入采样频率 （50 MHz） 和时钟频率 （150 MHz）。另一方面，第二级采用 L2/M2=24/25 有理数速率变化，因此，FIR-Compiler设置与图6所示大同小异。此处COE文件名为dec_L24_M25_rad10.coe，插值速率值设为L2=24，而输入采样频率为12.5 MHz。

在布局布线之后，上述两个滤波级占用以下FPGA资源：

第一级（L1/M1= 1/4）：

Slice 触发器数量：321 个

Slice LUT数量：223 个

占用 Slice数量：62 个

DSP48 MAC单元数量：4 个

BRAM单元数量：0 个

第二级（L2/M2 = 24/25）：

Slice触发器数量：206 个

Slice LUT数量：209 个

占用 Slice数量：68 个

DSP48 MAC单元数量：3 个

BRAM单元数量：1 个

由于采用多级方法，与单级理想滤波器资源占用相比，我们现在可以节约 3% 左右的触发器，4%的LUT，15%的Slice，46%的DSP48以及83%的BRAM单元。尤其是我们只需少得多的MAC与BRAM单元，分别只有6个和5个。原因是第二个滤波器以更低的输入采样频率运行，而采用整数速率变化的第一个滤波器可以充分利用系数对称。

其它资源

我们在本辅导资料中介绍了两个降采样滤波器例子，一个是整数系数（50），另一个是有理数系数（25/6），而且

本文强调了在MATLAB设计滤波器以及采用FIR-Compiler和CIC-Compiler 在赛灵思FGPA中实现它们的方法。相关数据手册详细介绍采用CORE Generator实现滤波器所涉及的参数设置。