卡尔曼滤波应用实例

　　卡尔曼滤波的一个典型实例是从一组有限的，包含噪声的，对物体位置的观察序列（可能有偏差）预测出物体的位置的坐标及速度。在很多工程应用（如雷达、计算机视觉）中都可以找到它的身影。同时，卡尔曼滤波也是控制理论以及控制系统工程中的一个重要课题。

　　实例

　　一。 已知一物体作自由落体运动，对其高度进行了20次测量，测量值如下表

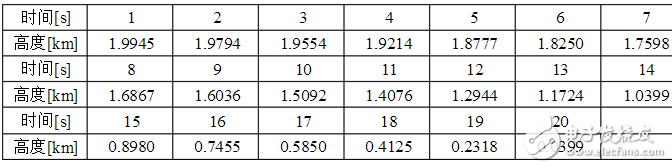
　　设高度的测量误差是均值为0、方差为1的高斯白噪声随机序列，该物体的初始高度0h和速度0V也是高斯分布的随机变量，且0000019001000，var10/02EhhmPEVmsV。试求该物体高度

　　和速度随时间变化的最优估计。（2/80.9smg）

　　解：

　　1. 令X（k）=hkXkvk）     t=1 R（k）=1 Q（k）=0

　　根据离散时间卡尔曼滤波公式，则有：

　　2.实验结果

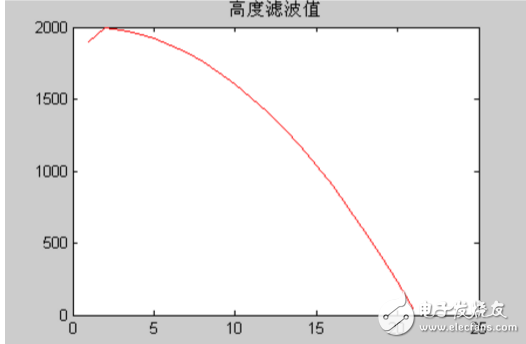
　　高度随时间变化估计

’

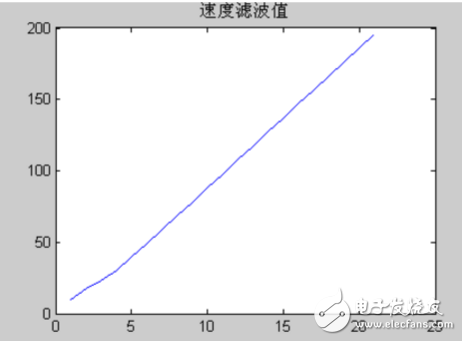
　　速度随时间变化的最优估计

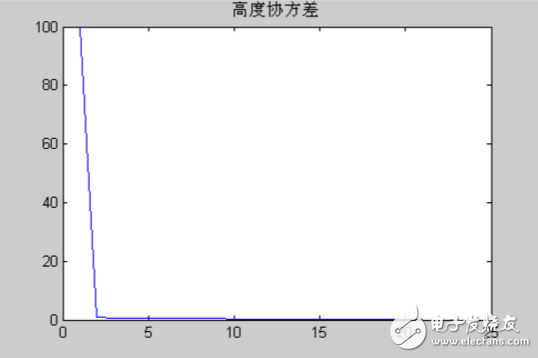
　　计高度协方差

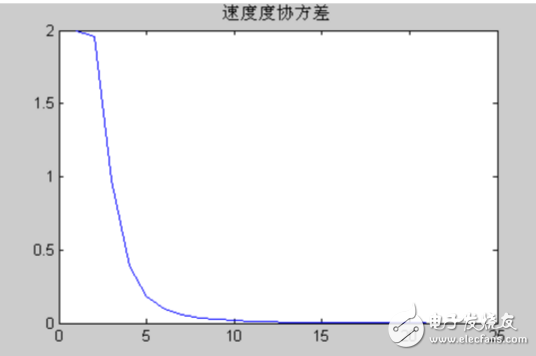
　　速度协方差

　　速度协方差从以上的结果，可以得到高度和速度的估计值，再通过所得到的高度协方差和速度协方差，可见用卡尔曼滤波法，虽然刚开始的初始高度协方差很大为100，但通过2步之后减小到不超过1，逐渐接近于0，同样的速度协方差刚开始的时候也比较大，为2，但是通过5步之后迅速减小，到10步之后接近于0。

　　3.有关参数的影响（例如初始条件、噪声统计特性对滤波结果的影响等）；

　　1）初始条件改变时，改变初始高度值，和速度值 00230030/EhmEVms

　　由实验结果分析可得

　　度滤波值和速度滤波值在开始几步接近初始值，协方差值基本不变。