理解FFT和信号加窗原理及意义

学习信号时域和频域、快速傅立叶变换(FFT)、加窗，以及如何通过这些 *** 作来加深对信号的认识。

1. 理解时域、频域、FFT

傅立叶变换有助于理解常见的信号，以及如何辨别信号中的错误。 尽管傅立叶变换是一个复杂的数学函数，但是通过一个测量信号来理解傅立叶变换的概念并不复杂。 从根本上说，傅立叶变换将一个信号分解为不同幅值和频率的正弦波。 我们继续来分析这句话的意义所在。
 

所有信号都是若干正弦波的和

我们通常把一个实际信号看作是根据时间变化的电压值。 这是从时域的角度来观察信号。 傅立叶定律指出，任意波形在时域中都可以由若干个正弦波和余弦波的加权和来表示。 例如，有两个正弦波，其中一个的频率是另一个的3倍。 将两个正弦波相加，就得到了一个不同的信号。

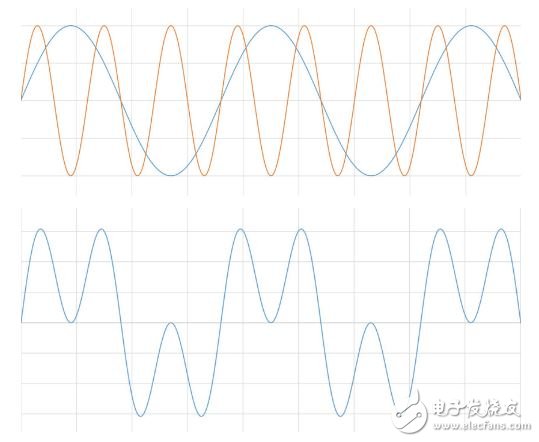
图1： 两个信号相加，得到一个新的信号。

假设第二号波形幅值也是第一个波形的1/3。 此时，只有波峰受影响。

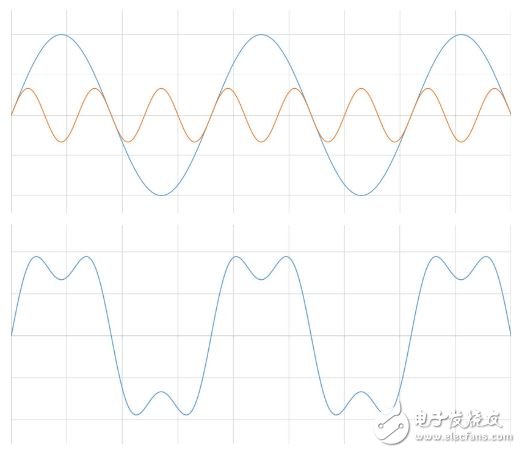
图2：信号相加时调整幅值影响波峰。

假加上一个幅值和频率只有原信号1/5的信号。 按这种方式一直加，直到触碰到噪声边界，您可能会认出结果波形。

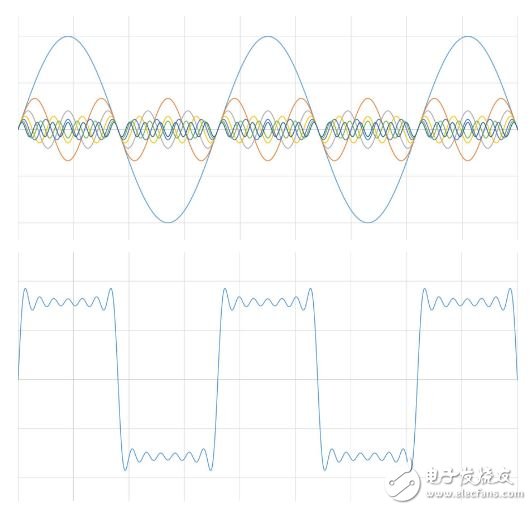
图3：方波是若干正弦波的和。

您创建了一个方波。 通过这种方法，所有时域中的信号都可表示为一组正弦波。

即使可以通过这种方法构造信号，那意味着什么呢？ 因为可以通过正弦波构造信号，同理也可以将信号分解为正弦波。 一旦信号被分解，可查看和分析原信号中不同频率的信号。 请参考信号分解的下列使用实例：

分解广播信号，可选择要收听的特定频率（电台）。

将声频信号分解为不同频率的信号（例如，低音、高音），可增强特定频段，移除噪声。

根据速度和强度分解地震波形，可优化楼宇设计，避免强烈震动。

分解计算机数据时，可忽略频率重要性最低的数据，这样就能更紧凑地利用内存。这就是文件压缩的原理。

使用FFT分解信号

傅立叶变换将一个时域信号转换为频域信号。 频域信号显示了不同频率对应的电压。 频域是另一种观察信号的角度。

数字化仪对波形进行采样，然后将采样转换为离散的值。 因为发生了转换，傅立叶转换在这些数据上无法进行。 可使用离散傅立叶变换(DFT)，其结果是离散形式的频域信号。 FFT是DFT的一种优化实现，计算量较少，但是本质上是对信号的分解。

请查看上图1中的信号。 有两个频率不同的信号。在该情况下，频域中就会显示两条表示不同频率的竖线。

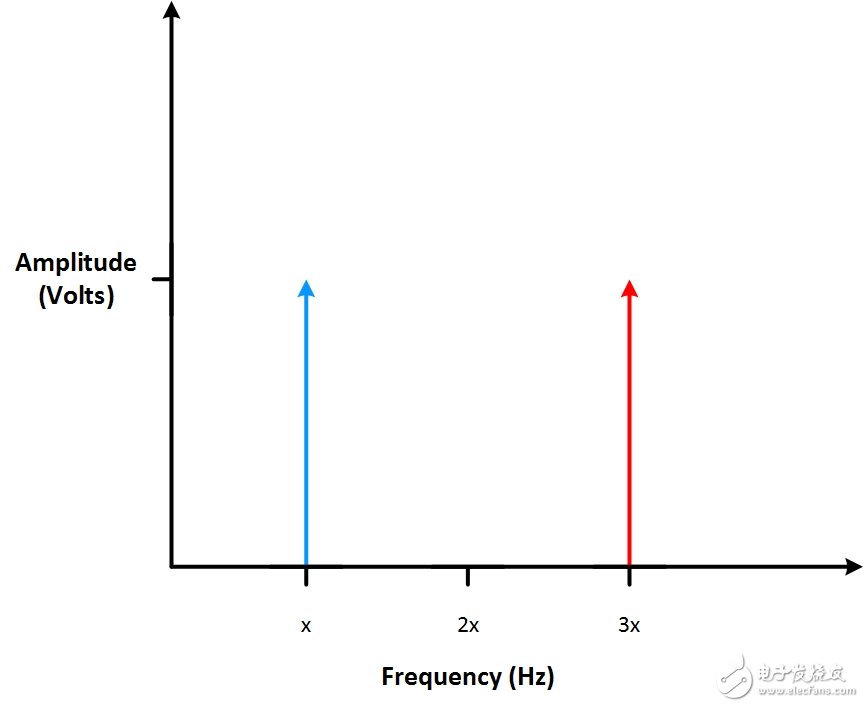
图4：当相同幅值的两个正弦波相加，在频域中就显示为两条频率竖线。

原信号的幅值在竖轴上表示。 图2中有个不同幅值的信号。频域中最高的竖线对应于最高电压的正弦信号。 在频域里观察信号，可直观地看出最高电压发生在哪个频率上。

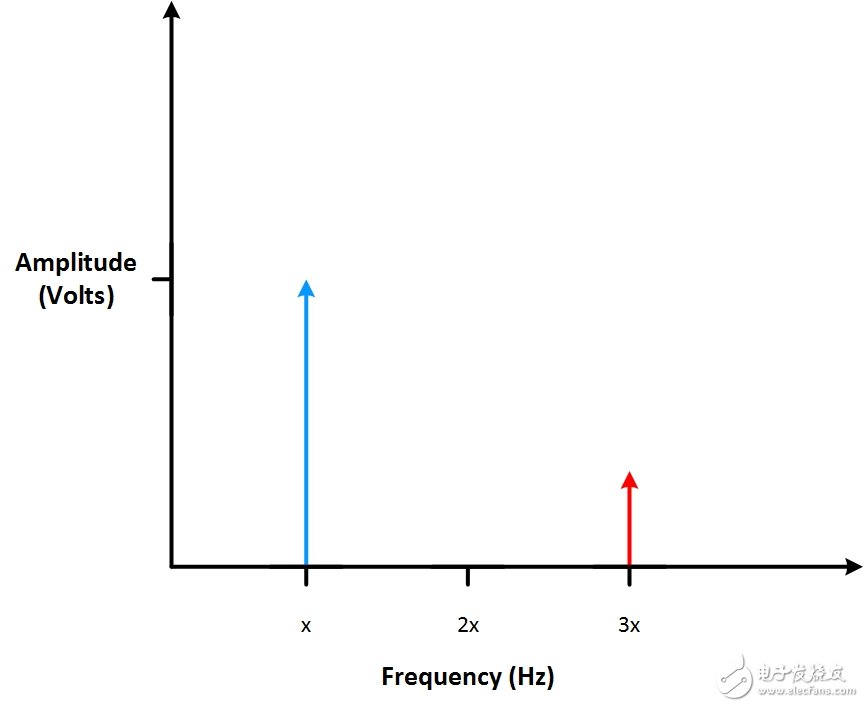
图5： 最高的竖线是幅值最大的频率。

在频域里也可观察到信号的形状。 例如，频域中方波信号的形状。 使用不同频率的正弦波创建一个方波。即可预见，在频域中，这些信号都会被表示为一根竖线，每一根竖线都表示组成方波的正弦波。 如频域中，竖线显示为一个梯度，就可知道原信号是一个方波信号。

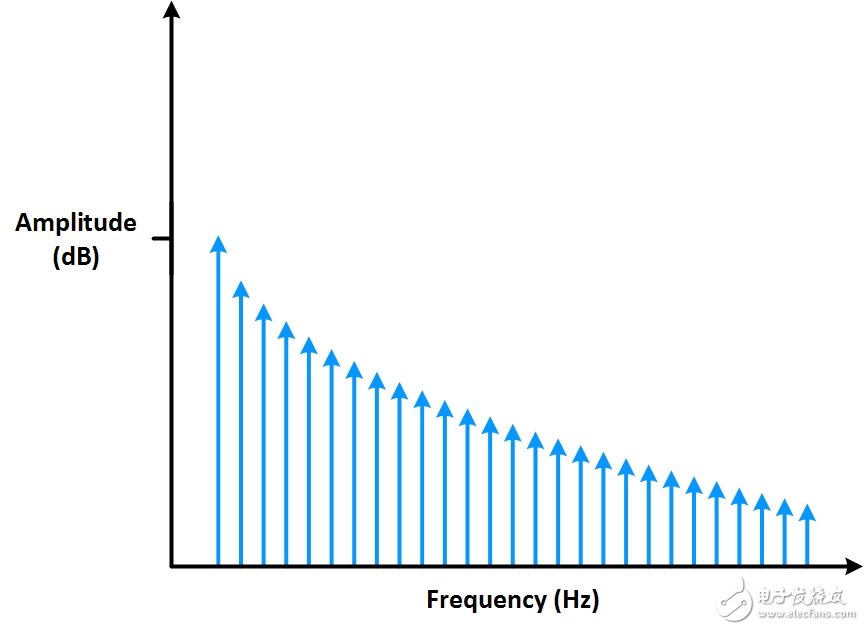
图6： 频域中表示正弦波的竖线呈现为一个梯度。