使用2×4 MIMO-OFDM系统模型下的K-Best算法设计的K-Best检测器

摘 要： 基于贝尔实验室V-BLAST结构构建了2×4 MIMO-OFDM系统模型，并确定了该模型下K-Best算法的K值。之后对K-Best检测器进行了硬件架构设计，采用Xilinx Virtex-5芯片对所设计检测器加以实现，并给出检测器资源消耗和时钟频率等性能指标，最后通过仿真验证检测器正确性。

 

MIMO-OFDM系统接收端检测算法中，最大似然检测（Maximum Likelihood，ML）算法具有最优检测性能，但其复杂度会随着天线数量和调制阶数增加呈指数增长。K-Best算法[1]克服了ML算法复杂度较高的缺点，并且能够取得与ML算法相似的误比特率（Bit Error Rate，BER）性能，因而受到广泛关注。

目前已实现的K-Best检测器主要分为专用集成电路(ApplicaTIon Specific Integrated Circuit，ASIC)[2-3]和现场可编程门阵列(Field Programmable Gate Array，FPGA)[4]两类。其中：参考文献[2]设计并实现吞吐率达到424 Mb/s的K-Best检测器。参考文献[3]中的半径自适应K-Best算法结合了深度球形解码和宽度球形解码的特点，以较低的功耗和硬件资源消耗达到了252 Mb/s的数据吞吐率。而后参考文献[4]改进了K-Best算法对路径度量的排序方法，并基于FPGA实现了K+-Best检测器，其数据吞吐率达到455 Mb/s。上述K-Best检测器均用于4×4天线系统中，并需设置较大的K值以获得较高的BER性能。

本文首先介绍了K-Best算法基本原理，然后在构建的2×4(2根发送天线、4根接收天线)MIMO-OFDM系统中仿真确定了K-Best算法中的K值，之后对K-Best检测器进行了硬件架构设计，最后采用FPGA对所设计检测器进行编程实现，给出检测器资源消耗和时钟频率等性能指标，并通过仿真验证了检测器的正确性。

1 K-Best算法分析

1.1 算法原理

假设在一个MIMO-OFDM系统中配置M根发送天线和N根接收天线(N≥M)，则该系统的信号模型可以表示为：

y=Hs+n(1)

其中，s为M维发送信号，y为N维接收信号，n为N维加性高斯白噪声。信道矩阵H是复数域的N×M维矩阵。为避免复数运算带来额外硬件开销，可将信号模型（1）实数化分解：

R(y)I(y)=R(H) I(H)I(H) R(H)R(s)I(s)+R(n)I(n)(2)

其中，R(?驻)和I(?驻)分别表示复数?驻的实部与虚部。实数化后的信号模型由式（3）表示：

然后对信道矩阵实施QR分解，即H=QR，采用最大似然准则求解（3）可得：

其中，Q为2N×2N维正交矩阵；R为2N×2M维矩阵；y=QTy为2N维向量；为实数化后的星座点集合，例如采用4QAM调制时，星座集合为{-1，1}。

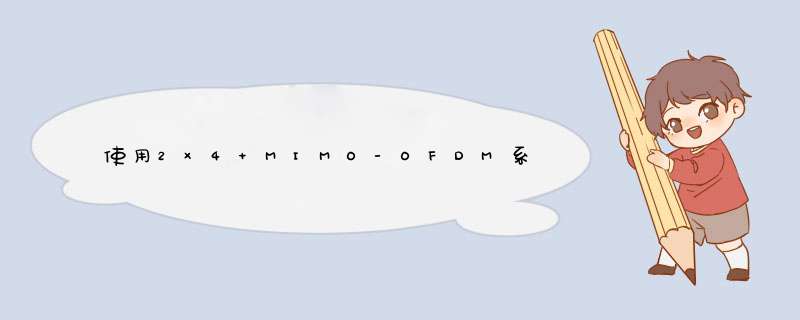
根据式（4）可得，K-Best算法的检测过程可以近似为图1所示的树形结构。定义参数K为每层保留节点个数，检测过程从第2M层开始，各层需计算欧式距离增量（INC），并与上一层累积欧式距离（PED）相加得到当前层的PED，然后将PED进行排序判决，保留其中较小的K条PED和其对应的K个节点，删除废弃节点的所有信息。当检测到最后一层时，从保留的K条PED再次选出最小累积欧式距离，并将其对应的节点作为检测结果。可以看出，K-Best算法中的K值对算法最终的BER性能和复杂度起着关键性作用。

1.2 K-Best算法K值的确定

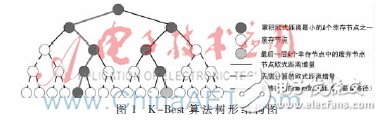
贝尔实验室提出的垂直分层空时结构(VerTIcal-BLAST，V-BLAST)是MIMO空间复用的典型代表[5]，具有时延小、处理简单等特点。本文基于V-BLAST构建的2×4 MIMO-OFDM系统模型如图2所示。

图3为在上述系统中对K-Best算法的BER性能仿真结果。从图中可以看出，当收发天线为4×4且分别设置K=1、2时，算法BER性能较差；只有当K=16时，算法BER性能才与ML算法性能一致（此时已遍历整个树形结构中的所有节点），故该复用方案下K值大小对算法BER性能影响很大。而当收发天线数为2×4，则只有K=1时算法BER性能较差，K=2时获得的BER性能与K=10和ML算法性能基本一致，故在后续的K-Best检测器FPGA实现中将K值设为2。

2 K-Best算法的硬件实现

2.1 QR分解模块