步进电机静态转矩特性的测量方法

　　步进电机静态转矩特性

　　步进电机的线圈通直流电时，带负载转子的电磁转矩（与负载转矩平衡而产生的恢复电磁转矩称为静态转矩或静止转矩）与转子功率角的关系称为角度-静止转矩特性，这就是电机的静态特性。如下图所示：

　　

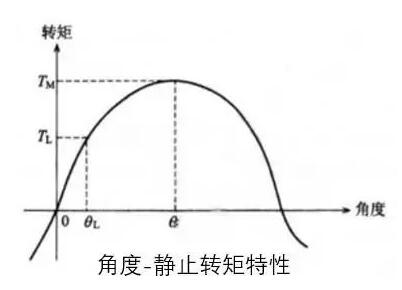
　　因为转子为永磁体，产生的气隙磁密为正弦分布，所以理论上静止转矩曲线为正弦波。此角度-静止转矩特性为步进电机产生电磁转矩能力的重要指标，最大转矩越大越好，转矩波形越接近正弦越好。实际上磁极下存在齿槽转矩，使合成转矩发生畸变，如两相电机的齿槽转矩为静止转矩角度周期的4倍谐波，加在正弦的静止转矩上，则上图所示的转矩为：

　　TL=TMsin［（θL/θM）π/2］

　　其中TL与TM各表示负载转矩和最大静止转矩（或称把持转矩），相对应的功率角为θL和θM，此位移角的变化决定了步进电机位置精度。根据上式得到：

　　θL=（2θM/π）arcsin（TL/TM）

　　PM型永磁步进电机和HB混合式步进电机的步距角θs在前面的课程中讲过即：θs=180°/PNr，角度改为机械角度（弧度），则变成下式：

　　θs=π/（2Nr）

　　上式Nr为转子齿数或极对数，所以两相电机θM=θs。

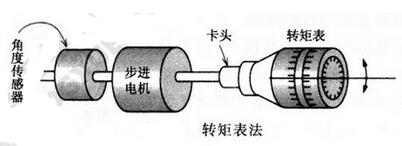
　　步进电机静态转矩特性的测量方法

　　转矩表：将步进电机固定。如图下图所示，读取转矩表的读数和角度测量仪的读数，依据角度及转矩绘制距角特性曲线，如图如本文前面第一图所示。如不测量角度，只能测出最大静态转矩TM。

　　

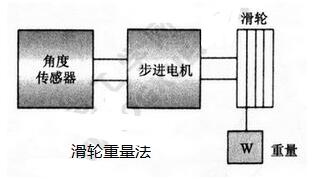
　　滑轮重量法：如图下图所示，用滑轮和重物代替上图的转矩表。依次改变重物W的重量，利用电位计或编码器测量角度，也能得到与转矩表相同的转矩曲线。

　　

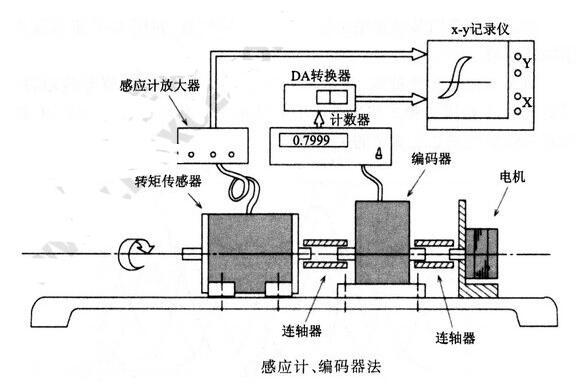
　　应力计和编码器：前述的两种方法转矩值需要人工读取，测量费时间，且无法自动得出转矩曲线。相对的，如图下图所示，应变计式转矩计与光学式两轴编码器直接与步进电机连接，利用转矩计、编码器和记录仪，能连续测量静态转矩特性。

　　

　　为了使电机旋转，须使用减速器降低电机转速，齿轮啮合引起的重量变化量很小，此时，须加上比转子惯量大十几倍的飞轮。在齿轮的负载方向要加上重量，以便使齿隙最小。下图的曲线为图上图的方法的试验曲线，调整被试电机的供电电压，测量静态转矩特性。被试电机的尺寸大小为42mm，33mm长，两相HB型，1.8°，35Ω/相，转子惯量15g•cm2。

　　

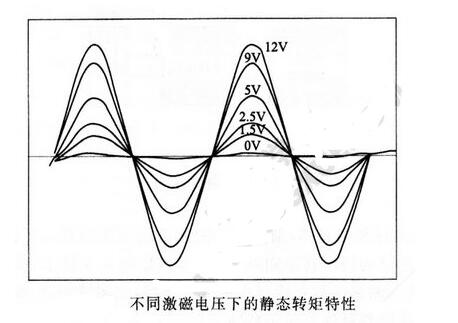
　　测量时需要用基准重量来校正Y轴的转矩值，利用X-Y记录仪直接读取转矩值。

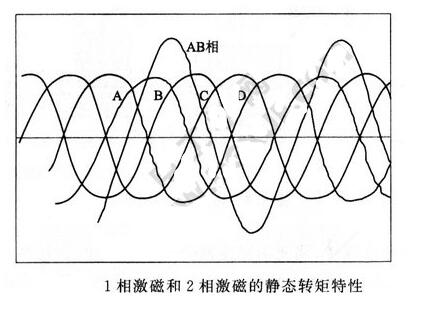
　　下图为改变激磁相，测量1相激磁和2相激磁的静态转矩特性。可以看出，1相激磁和2相激磁产生的转矩大小和停止位置的不同，即相位差和转矩与图本文第二图所示的关系相同。