
随着大数据时代的到来,机器学习成为解决问题的一种重要且关键的工具。不管是工业界还是学术界,机器学习都是一个炙手可热的方向,但是学术界和工 业界对机器学习的研究各有侧重,学术界侧重于对机器学习理论的研究,工业界侧重于如何用机器学习来解决实际问题。我们结合美团在机器学习上的实践,进行一 个实战(InAcTIon)系列的介绍(带“机器学习InAcTIon系列”标签的文章),介绍机器学习在解决工业界问题的实战中所需的基本技术、经验和 技巧。本文主要结合实际问题,概要地介绍机器学习解决实际问题的整个流程,包括对问题建模、准备训练数据、抽取特征、训练模型和优化模型等关键环节;另外 几篇则会对这些关键环节进行更深入地介绍。
下文分为1)机器学习的概述,2)对问题建模,3)准备训练数据,4)抽取特征,5)训练模型,6)优化模型,7)总结 共7个章节进行介绍。
机器学习的概述:什么是机器学习?随着机器学习在实际工业领域中不断获得应用,这个词已经被赋予了各种不同含义。在本文中的“机器学习”含义与wikipedia上的解释比较契 合,如下:Machine learning is a scienTIfic discipline that deals with the construcTIon and study of algorithms that can learn from data.
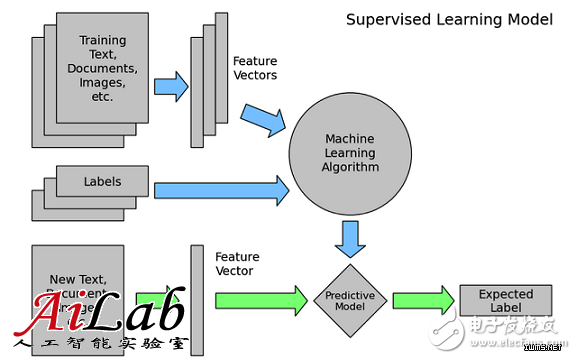
机器学习可以分为无监督学习(unsupervised learning)和有监督学习(supervised learning),在工业界中,有监督学习是更常见和更有价值的方式,下文中主要以这种方式展开介绍。如下图中所示,有监督的机器学习在解决实际问题 时,有两个流程,一个是离线训练流程(蓝色箭头),包含数据筛选和清洗、特征抽娶模型训练和优化模型等环节;另一个流程则是应用流程(绿色箭头),对需 要预估的数据,抽取特征,应用离线训练得到的模型进行预估,获得预估值作用在实际产品中。在这两个流程中,离线训练是最有技术挑战的工作(在线预估流程很 多工作可以复用离线训练流程的工作),所以下文主要介绍离线训练流程。
模型,是机器学习中的一个重要概念,简单的讲,指特征空间到输出空间的映射;一般由模型的假设函数和参数w组成(下面公式就是Logistic Regression模型的一种表达,在训练模型的章节做稍详细的解释);一个模型的假设空间(hypothesis space),指给定模型所有可能w对应的输出空间组成的集合。工业界常用的模型有Logistic Regression(简称LR)、Gradient Boosting Decision Tree(简称GBDT)、Support Vector Machine(简称SVM)、Deep Neural Network(简称DNN)等。
模型训练就是基于训练数据,获得一组参数w,使得特定目标最优,即获得了特征空间到输出空间的最优映射,具体怎么实现,见训练模型章节。
为什么要用机器学习解决问题?目前处于大数据时代,到处都有成T成P的数据,简单规则处理难以发挥这些数据的价值;
廉价的高性能计算,使得基于大规模数据的学习时间和代价降低;
廉价的大规模存储,使得能够更快地和代价更小地处理大规模数据;
存在大量高价值的问题,使得花大量精力用机器学习解决问题后,能获得丰厚收益。
机器学习应该用于解决什么问题?目标问题需要价值巨大,因为机器学习解决问题有一定的代价;
目标问题有大量数据可用,有大量数据才能使机器学习比较好地解决问题(相对于简单规则或人工);
目标问题由多种因素(特征)决定,机器学习解决问题的优势才能体现(相对于简单规则或人工);
目标问题需要持续优化,因为机器学习可以基于数据自我学习和迭代,持续地发挥价值。
对问题建模本文以DEAL(团购单)交易额预估问题为例(就是预估一个给定DEAL一段时间内卖了多少钱),介绍使用机器学习如何解决问题。首先需要:
收集问题的资料,理解问题,成为这个问题的专家;
拆解问题,简化问题,将问题转化机器可预估的问题。
深入理解和分析DEAL交易额后,可以将它分解为如下图的几个问题:
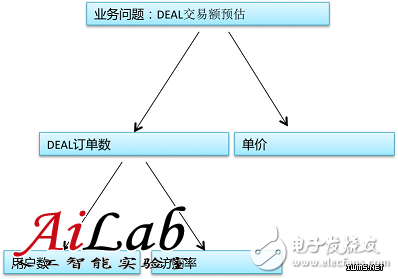 单个模型?多个模型?如何来选择?
单个模型?多个模型?如何来选择?
按照上图进行拆解后,预估DEAL交易额就有2种可能模式,一种是直接预估交易额;另一种是预估各子问题,如建立一个用户数模型和建立一个访购率模型(访问这个DEAL的用户会购买的单子数),再基于这些子问题的预估值计算交易额。
不同方式有不同优缺点,具体如下:
模式缺点优点
单模型 1. 预估难度大2. 风险比较高 1. 理论上可以获得最优预估(实际上很难)2. 一次解决问题
多模型 1. 可能产生积累误差2. 训练和应用成本高 1. 单个子模型更容易实现比较准地预估2. 可以调整子模型的融合方式,以达到最佳效果
1)问题可预估的难度,难度大,则考虑用多模型;
2)问题本身的重要性,问题很重要,则考虑用多模型;
3)多个模型的关系是否明确,关系明确,则可以用多模型。
如果采用多模型,如何融合?可以根据问题的特点和要求进行线性融合,或进行复杂的融合。以本文问题为例,至少可以有如下两种:
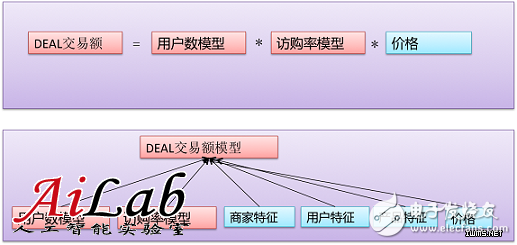
对于DEAL交易额这个问题,我们认为直接预估难度很大,希望拆成子问题进行预估,即多模型模式。那样就需要建立用户数模型和访购率模型,因为机器学习解决问题的方式类似,下文只以访购率模型为例。要解决访购率问题,首先要选择模型,我们有如下的一些考虑:
主要考虑1)选择与业务目标一致的模型;
2)选择与训练数据和特征相符的模型。
训练数据少,High Level特征多,则使用“复杂”的非线性模型(流行的GBDT、Random Forest等);训练数据很大量,Low Level特征多,则使用“简单”的线性模型(流行的LR、Linear-SVM等)。
补充考虑1)当前模型是否被工业界广泛使用;
2)当前模型是否有比较成熟的开源工具包(公司内或公司外);
3)当前工具包能够的处理数据量能否满足要求;
4)自己对当前模型理论是否了解,是否之前用过该模型解决问题。
为实际问题选择模型,需要转化问题的业务目标为模型评价目标,转化模型评价目标为模型优化目标;根据业务的不同目标,选择合适的模型,具体关系如下:
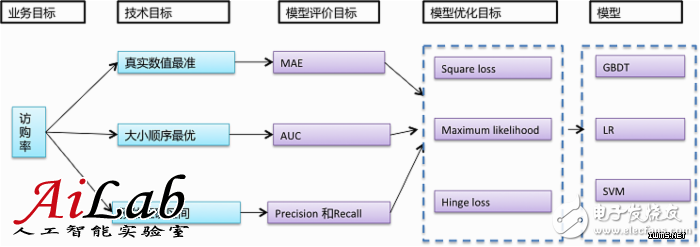
通常来讲,预估真实数值(回归)、大小顺序(排序)、目标所在的正确区间(分类)的难度从大到小,根据应用所需,尽可能选择难度小的目标进行。 对于访购率预估的应用目标来说,我们至少需要知道大小顺序或真实数值,所以我们可以选择Area Under Curve(AUC)或Mean Absolute Error(MAE)作为评估目标,以Maximum likelihood为模型损失函数(即优化目标)。综上所述,我们选择spark版本 GBDT或LR,主要基于如下考虑:
1)可以解决排序或回归问题;
2)我们自己实现了算法,经常使用,效果很好;
3)支持海量数据;
4)工业界广泛使用。
准备训练数据深入理解问题,针对问题选择了相应的模型后,接下来则需要准备数据;数据是机器学习解决问题的根本,数据选择不对,则问题不可能被解决,所以准备训练数据需要格外的小心和注意:
注意点:
待解决问题的数据本身的分布尽量一致;
训练集/测试集分布与线上预测环境的数据分布尽可能一致,这里的分布是指(x,y)的分布,不仅仅是y的分布;
y数据噪音尽可能小,尽量剔除y有噪音的数据;
非必要不做采样,采样常常可能使实际数据分布发生变化,但是如果数据太大无法训练或者正负比例严重失调(如超过100:1),则需要采样解决。
常见问题及解决办法待解决问题的数据分布不一致:
1)访购率问题中DEAL数据可能差异很大,如美食DEAL和酒店DEAL的影响因素或表现很不一致,需要做特别处理;要么对数据提前归一化,要么将分布不一致因素作为特征,要么对各类别DEAL单独训练模型。
数据分布变化了:
1)用半年前的数据训练模型,用来预测当前数据,因为数据分布随着时间可能变化了,效果可能很差。尽量用近期的数据训练,来预测当前数据,历史的数据可以做降权用到模型,或做transfer learning。
y数据有噪音:
1)在建立CTR模型时,将用户没有看到的Item作为负例,这些Item是因为用户没有看到才没有被点击,不一定是用户不喜欢而没有被点击,所以这些 Item是有噪音的。可以采用一些简单规则,剔除这些噪音负例,如采用skip-above思想,即用户点过的Item之上,没有点过的Item作为负例 (假设用户是从上往下浏览Item)。
采样方法有偏,没有覆盖整个集合:
1)访购率问题中,如果只取只有一个门店的DEAL进行预估,则对于多门店的DEAL无法很好预估。应该保证一个门店的和多个门店的DEAL数据都有;
2)无客观数据的二分类问题,用规则来获得正/负例,规则对正/负例的覆盖不全面。应该随机抽样数据,进行人工标注,以确保抽样数据和实际数据分布一致。
访购率问题的训练数据收集N个月的DEAL数据(x)及相应访购率(y);
收集最近N个月,剔除节假日等非常规时间 (保持分布一致);
只收集在线时长>T 且 访问用户数 > U的DEAL (减少y的噪音);
考虑DEAL销量生命周期 (保持分布一致);
考虑不同城市、不同商圈、不同品类的差别 (保持分布一致)。
抽取特征完成数据筛选和清洗后,就需要对数据抽取特征,就是完成输入空间到特征空间的转换(见下图)。针对线性模型或非线性模型需要进行不同特征抽取,线性模型需要更多特征抽取工作和技巧,而非线性模型对特征抽取要求相对较低。
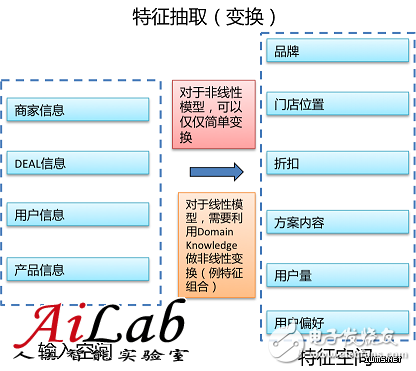
通常,特征可以分为High Level与Low Level,High Level指含义比较泛的特征,Low Level指含义比较特定的特征,举例来说:
DEAL A1属于POIA,人均50以下,访购率高;DEAL A2属于POIA,人均50以上,访购率高;DEAL B1属于POIB,人均50以下,访购率高;DEAL B2属于POIB,人均50以上,访购率底;
基于上面的数据,可以抽到两种特征,POI(门店)或人均消费;POI特征则是Low Level特征,人均消费则是High Level特征;假设模型通过学习,获得如下预估:
如果DEALx 属于POIA(Low Level feature),访购率高;如果DEALx 人均50以下(High Level feature),访购率高。
所以,总体上,Low Level 比较有针对性,单个特征覆盖面小(含有这个特征的数据不多),特征数量(维度)很大。High Level比较泛化,单个特征覆盖面大(含有这个特征的数据很多),特征数量(维度)不大。长尾样本的预测值主要受High Level特征影响。高频样本的预测值主要受Low Level特征影响。
对于访购率问题,有大量的High Level或Low Level的特征,其中一些展示在下图:
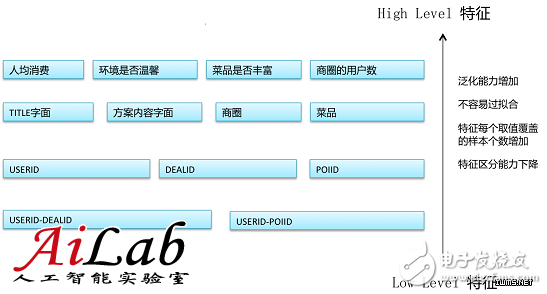 非线性模型的特征
非线性模型的特征
1)可以主要使用High Level特征,因为计算复杂度大,所以特征维度不宜太高;
2)通过High Level非线性映射可以比较好地拟合目标。
线性模型的特征
1)特征体系要尽可能全面,High Level和Low Level都要有;
2)可以将High Level转换Low Level,以提升模型的拟合能力。
特征归一化
特征抽取后,如果不同特征的取值范围相差很大,最好对特征进行归一化,以取得更好的效果,常见的归一化方式如下:
Rescaling:
归一化到[0,1] 或 [-1,1],用类似方式:
Standardization:
设为x分布的均值,
为x分布的标准差;
Scaling to unit length:
归一化到单位长度向量
特征选择
特征抽取和归一化之后,如果发现特征太多,导致模型无法训练,或很容易导致模型过拟合,则需要对特征进行选择,挑选有价值的特征。
Filter:假设特征子集对模型预估的影响互相独立,选择一个特征子集,分析该子集和数据Label的关系,如果存在某种正相关,则认为该特征子集有效。衡量特征子集和数据Label关系的算法有很多,如Chi-square,Information Gain。
Wrapper:选择一个特征子集加入原有特征集合,用模型进行训练,比较子集加入前后的效果,如果效果变好,则认为该特征子集有效,否则认为无效。
Embedded:将特征选择和模型训练结合起来,如在损失函数中加入L1 Norm ,L2 Norm。
训练模型
完成特征抽取和处理后,就可以开始模型训练了,下文以简单且常用的Logistic Regression模型(下称LR模型)为例,进行简单介绍。
设有m个(x,y)训练数据,其中x为特征向量,y为label,;w为模型中参数向量,即模型训练中需要学习的对象。
所谓训练模型,就是选定假说函数和损失函数,基于已有训练数据(x,y),不断调整w,使得损失函数最优,相应的w就是最终学习结果,也就得到相应的模型。
模型函数 1)假说函数,即假设x和y存在一种函数关系:
2)损失函数,基于上述假设函数,构建模型损失函数(优化目标),在LR中通常以(x,y)的最大似然估计为目标:
优化算法
梯度下降(Gradient Descent)
即w沿着损失函数的负梯度方向进行调整,示意图见下图,
的梯度即一阶导数(见下式),梯度下降有多种类型,如随机梯度下降或批量梯度下降。
随机梯度下降(Stochastic Gradient Descent),每一步随机选择一个样本
,计算相应的梯度,并完成w的更新,如下式,
批量梯度下降(Batch Gradient Descent),每一步都计算训练数据中的所有样本对应的梯度,w沿着这个梯度方向迭代,即

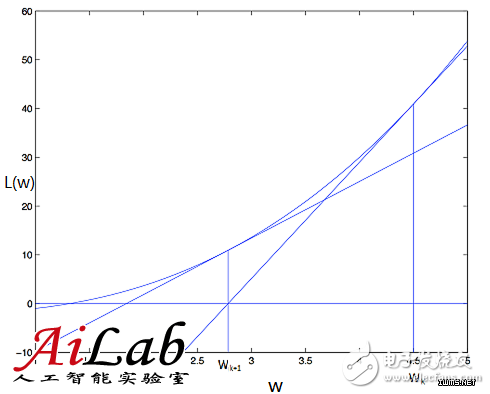
牛顿法(Newton’s Method)
牛顿法的基本思想是在极小点附近通过对目标函数做二阶Taylor展开,进而找到L(w)的极小点的估计值。形象地讲,在wk处做切线,该切线与L(w)=0的交点即为下一个迭代点wk+1(示意图如下)。w的更新公式如下,其中目标函数的二阶偏导数,即为大名鼎鼎的Hessian矩阵。
拟牛顿法(Quasi-Newton Methods):计算目标函数的二阶偏导数,难度较大,更为复杂的是目标函数的Hessian矩阵无法保持正定;不用二阶偏导数而构造出可以近似Hessian矩阵的逆的正定对称阵,从而在"拟牛顿"的条件下优化目标函数。
BFGS: 使用BFGS公式对H(w)进行近似,内存中需要放H(w),内存需要O(m2)级别;
L-BFGS:存储有限次数(如k次)的更新矩阵
,用这些更新矩阵生成新的H(w),内存降至O(m)级别;
OWLQN: 如果在目标函数中引入L1正则化,需要引入虚梯度来解决目标函数不可导问题,OWLQN就是用来解决这个问题。
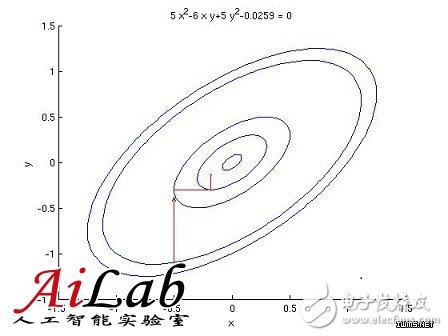
Coordinate Descent
对于w,每次迭代,固定其他维度不变,只对其一个维度进行搜索,确定最优下降方向(示意图如下),公式表达如下:
经过上文提到的数据筛选和清洗、特征设计和选择、模型训练,就得到了一个模型,但是如果发现效果不好?怎么办?
【首先】
反思目标是否可预估,数据和特征是否存在bug。
【然后】
分析一下模型是Overfitting还是Underfitting,从数据、特征和模型等环节做针对性优化。
Underfitting & Overfitting
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)