关于机器学习的前世今生和怎么用机器学习的方法去解决问题

Part 1: 机器学习的前世今生.

既然说机器学习，就从什么机器学习开始，相对而言，机器学习是一个比较泛的概念

初看的话，会觉得机器学习和人工智能，数据挖掘讲的东西很像，实际他们之间的关系可以概括为：

机器学习是人工智能的一个子方向

机器学习是数据挖掘的一种实现方式

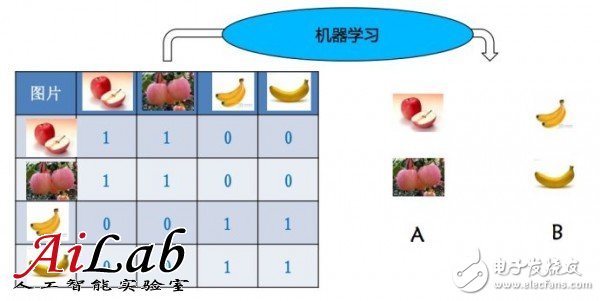
举个简单的例子，给一些苹果和香蕉，人会通过特征的判断做区分，并且记忆这些特征，下次来了一个新的苹果或者香蕉的时候，就可以判断是香蕉还是苹果了

作为任意一个算法或者说用程序执行的数学问题，总需要一些输入，一些输出

对于机器学习而言，输入就是特征所构成向量的向量，或者说是一个矩阵

如果只有一个特征，输入就是一个向量了，当然，向量是一个弱化的矩阵概念，统一称作矩阵

• 目前机器学习的核心技术是基于矩阵的优化技术

输入:矩阵 – 待学习的信息

输出:模型 – 总结出的规则

因此，目前主流的机器学习技术就可以形式化为

•输入:特征矩阵 X、标注向量 y

X 是特征矩阵,不包括“样本名称”和“样本 标注”

y 是标注向量,即“样本标注”那列

•输出:模型向量 w

•期望:X·w 尽可能接近 y

多种优化算法可以解 w,区别在于如何定义 “尽可能接近”

举个例子来说，要计算广告的CTR

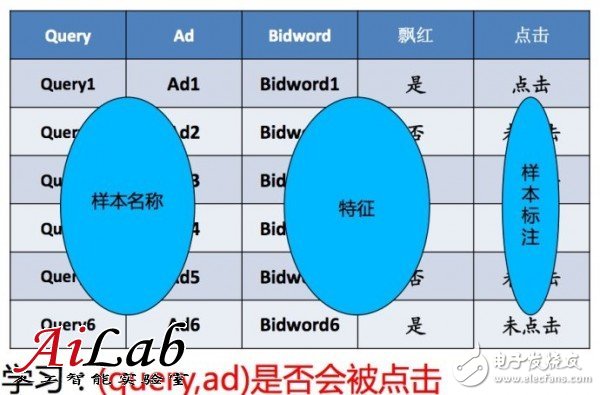
这个例子中

目标是要根据已知的auc特征，猜测这个目标广告是否会被点击

例子中特征只有两个，query关键词和“是否飘红”，判断结果是是否点击

好了，现在问题和输入输出都有了，具体解决这个问题，就可以选用相关的算法了

前面定义里面有这么一个隐含的关键点：X w 尽可能接近 y

如何定义这个“接近”，思路不同，算法就不同

比如对于LR (LogisTIc Regression)和SVM（Support Vector Machine）是不同的，作为样例，可以按照下图理解

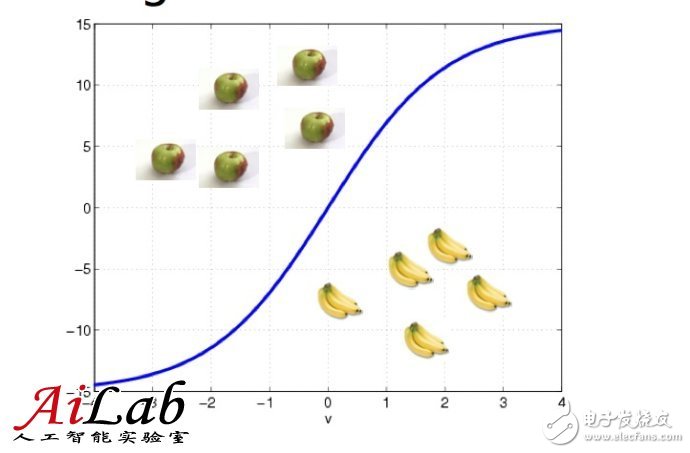
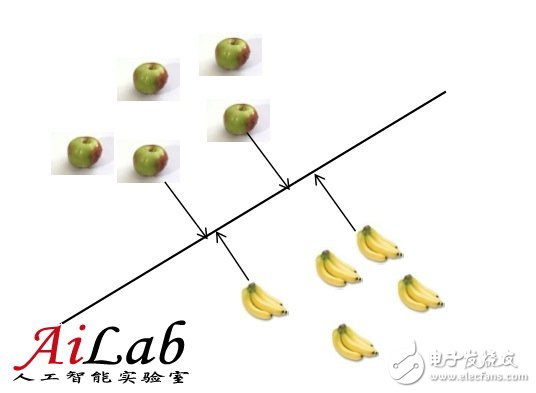
数学形式表示，就是

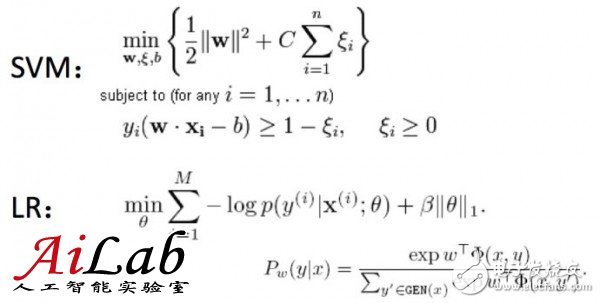
具体算法细节不是这里讨论的重点，在这两个算法中，“接近”的定义不同

学术的讲，就是“优化目标不同”

无论是否相同，我们都至少可以选一个优化目标了

有了优化目标，下面要做的就是如何求解这个优化目标了

一般现在用的思路主要是

L-BFGS，CDN，SGD这一些

把上面这一些要素放在一起，就有了完整的一个机器学习问题

Part 2: 如果你要用机器学习的方法去解决问题

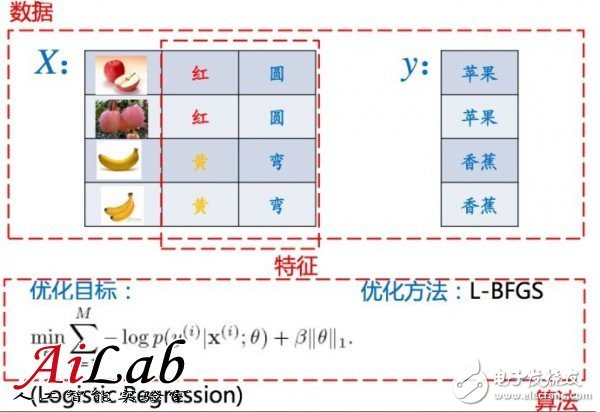
就需要注意三个方面的优化了：

算法，数据，特征

我们下面分开来说

算法，就是优化目标 + 优化算法

从优化目标的角度，工业界往往没有那个资源或者实力去研究新的算法，大多是在使用已有算法或者在已有算法的基础上做扩展

从优化算法的角度，主要是三点：

更小的计算代价

更快的收敛

更好的并行

这三点也比较好理解，对于一个工程问题，计算代价小，机器就可以做别的事情，更快的收敛，就可以更好的把结果投入使用，更好的并行，就可以用现有的大数据框架解决问题

训练数据，就是尽可能和实际同分布的数据 + 尽可能充分的数据

机器学习算法中，由于期望的往往是总的误差最小，所以很可能讲数据量小的类目判别错误

如果样本数据和实际数据分布差异大的话，对于实际的算法效果一般都不好

充分的数据，这个就好解释了，数据越充分，训练就越充分，就好比考试前做的练习越多，一般效果越好

特征，就是尽可能包含足够多的需要识别对象的信息

一个简单的例子，如果只有一个特征，对于水果的判断往往偏颇，就会造成下面的结果

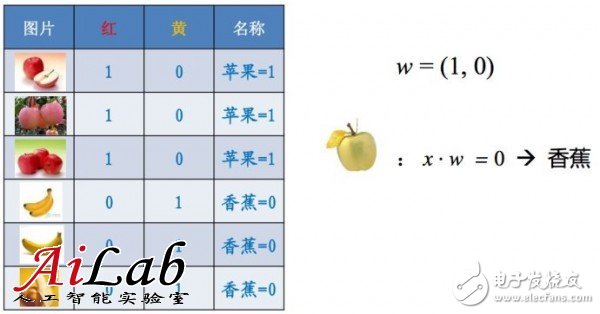
随着特征的增多，训练就会准确

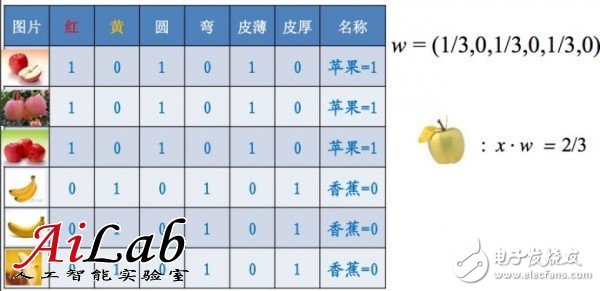
往往对于一个工程问题来说，特征是决定最多的方面

一个算法方面的优化，可能只是优化了2~3%的效果，但是特征可能就是50~60%了，一个工程项目七八成的精力往往都是画在特征选取上的，比如百度CTR预测，特征数据目前就是100亿级别的。

最后来说一点关于deep learning 的东西

Deep learning和目前的机器学习算法（Shallow Learning）最大的区别在于特征层数

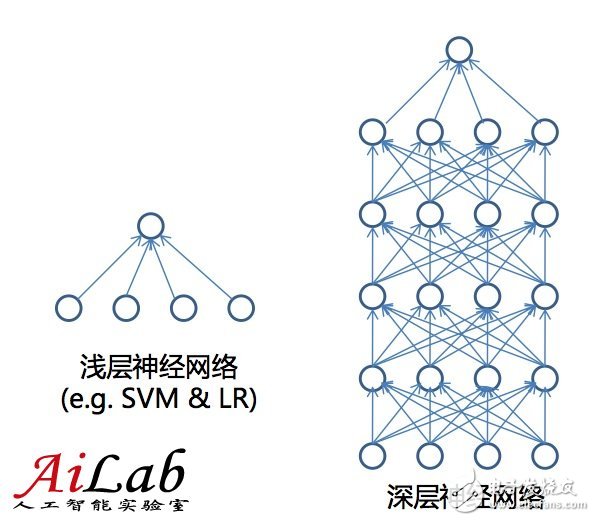
目前的机器学习算法主要是一层的，就是从特征直接推断是结果；

而Deep Learning和人类的处理问题的结果更接近，是由特征推断出一些中间层的结果，进而推断出最终结果的；

比如视觉是由一些点，进而判断出一些边，进而判断出一些形状，然后才是整体的物体的。

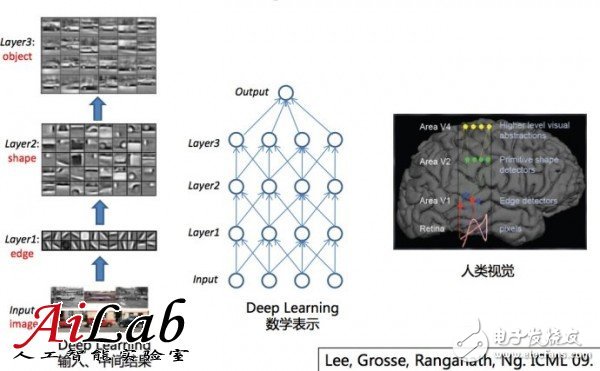
之前大量使用Shallow learning 主要是因为 Shallow Learning有很好的数学特征

解空间是凸函数

凸函数有大量的求解方法

凸函数优化可以参考

**Convex OpTImizaTIon

**

**~boyd/cvxbook/

而Deep Learning则容易找到局部最优解，而非全局最优解

Deep Learning解法可以参考

G. Hinton et al., A Fast Learning Algorithm for Deep Belief Nets. Neural ComputaTIon, 2006.

也可以看Andrew NG最近的课程

这里有最新的中文翻译http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程