
近年来,由于电力电子装置等非线性负荷的大量增加,电力系统的谐波污染越来越严重,严重地影响了电能计量的准确性和合理性,由此导致的纠纷也屡见不鲜。因此,研究用于电能计量的谐波电压源装置,对电能计量有着非常重要的意义。要求用于电能计量的谐波电压源能模拟21次内任意谐波的叠加,因此对采样频率要求较高。
目前,绝大多数谐波电压源装置采用开关功率放大器作为主电路,利用数字信号处理器(DigitalSignal Processing,DSP) 作为控制芯片。电力电子模型属于典型的高度并行模型,没有复杂的控制过程,但对采样率要求很高。开关器件的开关频率可达数百kHz,开关周期为μs 量级,实时系统要能稳定工作,其采样周期应小于开关周期的1 /10,DSP 则就有些显得力不从心了。
现场可编程门阵列(Field Programrnable GateArray,FPGA)采样率很高,适用于高速度要求的并行运算,运算过程简单。采用FPGA 执行运算,不仅能提高采样精度,还能节约成本。近年来,随着技术进步及市场需求量的增加,FPGA 产品单位货币所买到的MAC(乘法/累加运算)数比传统的DSP 还要高。200 万门FPGA 可达到1 280 亿/s MAC 的性能,比目前最快的DSP 性能还高一个量级,有取代DSP 之势。因此,将FPGA应用于谐波电压源的研究中,不失为一种好的思路。
VHS-ADC 是基于Matlab /Simulink 和FPGA的高速数字信号处理平台,采用Virtex-Ⅱ系列FPGA,内部拥有丰富的门资源与硬件乘法器,工作频率可达420 MHz,高速A/D 通道采样率可达105 MS /s,高速D/A 通道采样率可达125 MS /s。VHS-ADC 实现了与Simulink 的无缝连接。
本文在分析系统原理和设计系统参数基础上,在Simulink 中搭建了谐波电压源的连续域模型,并将其离散化,基于VHS-ADC 平台搭建了离散域仿真模型。
谐波电压源装置可模拟电网的各种现场情况,每相的谐波含量各不相同,因此主电路逆变部分采用3 个单相H 桥,每个单相H 桥由4 个开关管IGBT 组成。谐波电压源装置的主电路图如图1 所示。其中,每个H 桥可以等效为一个可控电压源,为系统提供频率、幅值、相位可调的谐波电压。逆变部分由4 个开关管IGBT 组成,逆变部分的直流侧电压由整流部分提供。整流部分由降压变压器和三相不可控整流电路组成,三相市电由降压变压器降压隔离,再经三相不可控整流,得到逆变电路所需的稳定直流电压。出口处的电感电容构成单调滤波器,用于滤除载波和高次谐波。
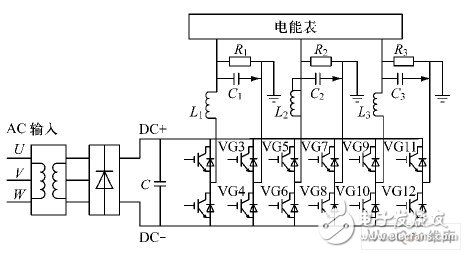
图1 谐波电压源装置主电路。
1. 2 谐波电压源的控制策略双闭环PI 调节的控制器简单,具有一定的鲁棒性,在工程控制领域得以广泛应用。因此,本文采用基于SPWM 的双闭环PI 控制策略,双闭环PI 控制的原理框图如图2 所示。图2 中,外环电压以理想的正弦波作为参考电压,输出电压与参考电压比较后经PI 调节作为电流内环的参考值,该电流参考值与反馈电流比较,再经PI 调节后与PWM 控制器中的三角波比较,产生PWM 信号驱动逆变器。
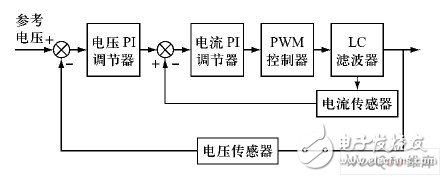
图2 电压、电流双闭环PI 控制原理框图。
本文引入负载电压瞬时值和滤波电容电流瞬时值作为反馈信号,根据实际值和期望值的偏差来实时控制输出电压波形,保证输出电压波形的精度,消除各种非正弦因素和扰动对输出电压的影响。由于输出滤波电容电流是对逆变器输出电压的微分,十分微小的电压变化即可引起电容电流的较大波动。因此,电容电流的引入更能使系统得到良好的动态性能。
2 基于VHS-ADC 平台的系统建模
基于FPGA 的VHS-ADC 高速信号处理平台,其模型库具有丰富的数字信号处理模型,Simulink自带的模型库不能编译成FPGA 代码,而Xilink模型库是基于离散信号z 域的模型。因此,需要构建z 域电力电子仿真模型。
基于z 域的控制电路VHS-ADC 模型如图3所示。该模型主要由PWM 发生器、PI 控制模块、限幅模块和死区模块组成。三角波用Counter 计数器产生。图3 中的Gateway in 为数据转化模块,将s 域信号转化为z 域信号。
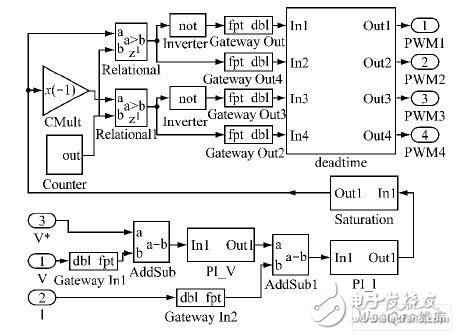
图3 控制电路VHS-ADC 模型。
电压外环PI 环节可表示为:
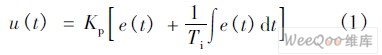
式中u(t)———控制量 e(t)———系统的控制偏差 TI———积分时间 Kp———比例系数 为了搭建离散域模型,在近似条件下得离散化方程为:
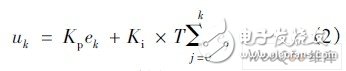
式中T———采样周期 k———采样序号,k = 1,2,… e(k)———PI 环节的输入信号 Ki = Kp /TI———积分系数 将式(2) 与uk - 1的表达式进行比较,则可得到第k 次采样时刻的离散方程:
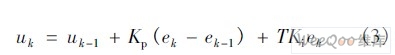
根据PI 的离散方程,可构建VHS-ADC 模型。 以电压外环PI 为例,其模型如图4 所示。CMult为乘法器模块,大小等于采样时间T;Convert 为数据转化模块,将输入信号转化为合理的数据格式。数据格式由数据位数和小数位数确定,在保证仿真精度的前提下,尽量减小数据位数,节约硬件资源。
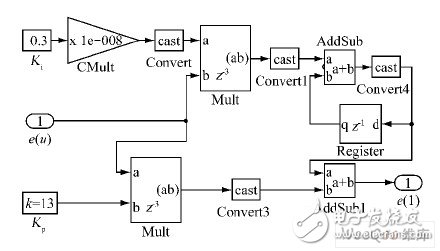
图4 电压外环PI 模型。
利用3 个加法器和1 个减法器,可实现限幅环节。减法器运算结果为负时,输出为0;运算结果为正时,输出为正常值。Constant1 和Constant2分别设置限幅模块的上、下限,限幅环节的模型如图5 所示。
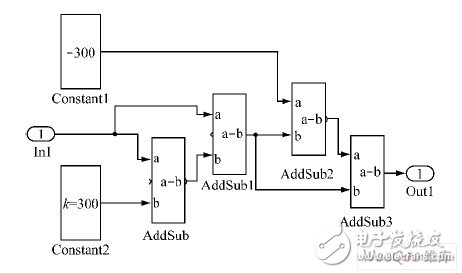
图5 限幅环节模型。
利用延迟模块和逻辑模块,可设置逆变器死区时间。输入信号经过Delay 模块,被延迟4 个采样周期时间,再与原信号进行逻辑与运算,就可得到带有死区时间的PWM 信号,被Delay 模块延迟的时间就是设置的死区时间。死区时间模型如图6 所示。
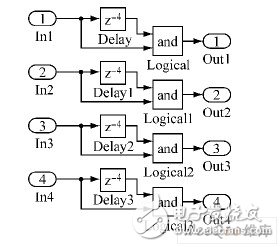
图6 死区时间的VHS-ADC 模型。
依靠平台提供的co-simulink 接口,将搭建的离散域控制模型进行编译,并自动生成代码,下载到FPGA,生成一个bit 流文件,将含有bit 文件的协议同仿真模块与谐波电压源的主电路连接。当在Simulink 中进行仿真时,FPGA 上的实时运算结果返回到Simulink 环境中,提高了仿真速度。
3 仿真结果
利用Matlab /Simulink 软件和VHS-ADC 仿真平台,建立完整的谐波电压源仿真模型。仿真参数:输入电压为Uu = Uv = Uw = 220 V;滤波电感L = 0. 05 mH,滤波电容C = 100 μF。电压环PI 参数:比例系数Kp = 13,Ki = 0. 4;电流环PI 参数:比例系数Kp = 15,Ki = 0. 2,负载R = 30 Ω;采样时间为100 ns,单相额定输出功率为3 kVA。
稳态下,谐波电压源输出的单相基波波形如图7 所示。因为三相不可控整流提供的直流电压需要约0. 01 s 才能达到稳定,所以谐波电压源输出波形在0. 01 s 之前是逐渐增大的,当直流电压稳定后,仿真波形几乎与期望波形重合。
为了验证装置的谐波合成能力,将30 V 4 次谐波叠加到100 V 基波上,如图8 所示。叠加后的波形在0. 01 s 前逐渐增大,在0. 01 s 后几乎与期望波形重叠;将所得波形进行傅里叶分析,4 次谐波含量为基波的30%,其频谱分析图如图9 所示。
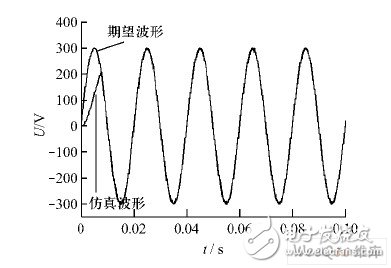
图7 基波输出波形与期望波形的对比。
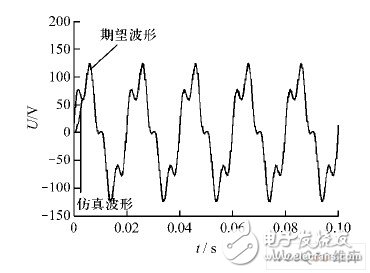
图8 叠加信号输出波形与期望波形的对比。
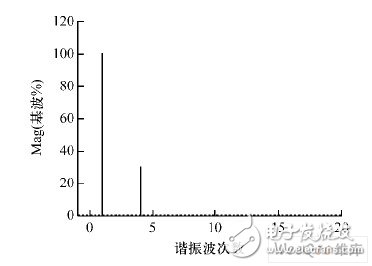
图9 叠加波形的频谱图。
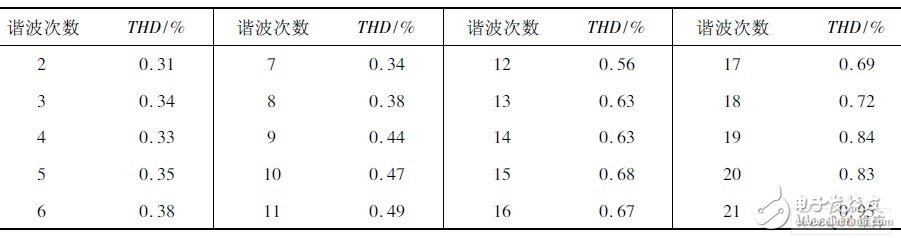
表1 为输出波形为单次谐波时,总谐波畸变率(THD)的大小。仿真结果表明,谐波电压源输出21 次内的单次谐波时,其THD 不会超过1%。
上述仿真结果说明了谐波电压源输出波形具有很高的精度,同时也验证了谐波电压源离散域模型的正确性。表1 谐波电压源输出单次谐波时的畸变率。
分析了谐波电压源的主电路模型,探讨了基于滤波电容电流和负载电压瞬时值的双闭环PI控制策略,利用VHS-ADC 数字信号处理系统采样率高、实时性强、建模灵活等特点,构建离散域实时仿真控制模型。仿真结果表明,该设计方法和离散化模型是正确的,说明了基于FPGA 进行谐波电压源研究的可行性。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)